In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130o and ∠ECD = 20⊙ Find ∠BAC.
Please refer to video for the figure.
Here, ∠BEC=130∘and∠ECD=20∘
∠AEB+∠BEC=180∘(Sum of angles formed by a straight line is 180^@)
∠AEB=180−130=50∘
Also, ∠ABD=∠ACD as these angles are subtended by a same chord on the circle.
So,∠ABD=∠ABE=20∘
Now, in ΔAEB
∠ABE+∠AEB+∠EAB=180∘
EAB+50+20=180
EAB=110∘
So, ∠BAC=EAB=110∘
Similar Questions
Knowledge Check
- Question 1 - Select One
A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC=130∘and∠ECD=20∘.∠BAC is
A(A) 120B(B)90∘C(C)100∘D(D)110∘
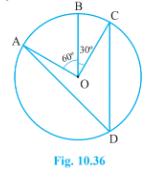
In Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC= 30o and ∠AOB= 60o. If D is a point on the circle other than the arc ABC, find ∠ADC.
 View Solution
View SolutionA, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn fig. 10, A,B,C and D are four points, and no three points are collinear. AC and BD intersect at O. there are eight triangle that you can observe. Name all the triangles.
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DEBC.
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionIn Fig. 4.179, ABC and DBC are on the same base BC . If AD and BC intersect at O , prove that Area (ABC)Area (DBC)=AODO (FIGURE)
View Solution

