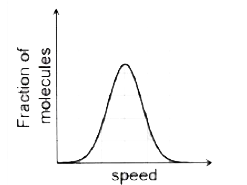
In the distribution of molecular speeds of a gas is as per the figure shown below, then the ratio of the most probale, the average, and the root mean square speeds, respectively, is

A

$1 : 1 : 1$

B

$1 : 1 : 1.224$

C

$1 : 1.128 : 1.224$

D

$1 : 1.128 : 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Due to symmetrical graph given, the average value of velocities will be at the middle, symmetrical velocity which is also most probable velocity.
While calculating rms speed, we have to take average of square of speeds and its root. In square of speeds, higher speeds will give more contribution so the value will be more than the average value.

|

Updated on:21/07/2023

Class 12 CHEMISTRY P BLOCK ELEMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The ratio of most probable velocity $(α)$ , average velocity $(¯ v)$ , root mean square velocity $(u)$ is
A $\sqrt{2} : \sqrt{\frac{8}{π}} : \sqrt{3}$
B $1 : \sqrt{2} : \sqrt{3}$
C $\sqrt{2} : \sqrt{3} : \sqrt{8}$
D $\sqrt{1} : \sqrt{8 π} : \sqrt{3}$
Question 2 - Select One
The ratio of everage speed, most probable speed and root mean square speed of a gas sample will be
A $\sqrt{\frac{4}{π}} : \sqrt{3} : \sqrt{2}$
B $\sqrt{\frac{8}{π}} : \sqrt{2} : \sqrt{3}$
C $\sqrt{\frac{16}{π}} : \sqrt{2} : \sqrt{3}$
D $\sqrt{2} : \sqrt{\frac{9}{π}} : \sqrt{3}$
Question 3 - Select One
The root mean square speed of gas molecules
Ais same for all gases at the same temperature
Bdepends on the mass of the gas molecule and its temperature
Cis independent of the density and pressure of the gas
Ddepends only on the temperature and volume of the gas

JEE ADVANCED PREVIOUS YEAR-JEE (ADVANCED ) 2020-SECTION -III

Home
Ask Doubt
Profile