Let a three- dimensional vector →V satissgy the condition , 2→V+→V×(ˆi+2ˆj)=2ˆi+ˆk.If3∣∣→V∣∣=√m . Then find the value of m.
The correct Answer is:6
2→V+→V×(ˆi+2ˆj)=(2ˆi+ˆk)
or2→V.(ˆi+2ˆj)+0=(2ˆi+ˆk).(ˆi+2ˆj)
or2→Vr.(ˆi+2ˆj)=2
or∣∣∣→V.(ˆi+2ˆj)2∣∣∣=1
or∣∣→V∣∣2.∣∣ˆi+2ˆj∣∣2cos2θ=1
(θ is the angle between →Vandˆi+2ˆj)
or∣∣→V∣∣25(1−sin2θ)=1
or∣∣→V∣∣25sin2θ=5∣∣→V∣∣2−1
from Eq. (i), we have
∣∣2→V+→V×(ˆi+2ˆj)∣∣2=∣∣2ˆi+ˆk∣∣2
or4∣∣→V∣∣2+∣∣→V×(ˆi+2ˆj)∣∣2=5
or4∣∣→V∣∣2+∣∣→V∣∣2.∣∣ˆi+2ˆj∣∣2sin2θ=5
or4∣∣→V∣∣2+5∣∣→V∣∣2sin2θ=5
or4∣∣→V∣∣2+5∣∣→V∣∣Y2−1=5
9∣∣→V∣∣2=6
or3∣∣→V∣∣=√6
=√6=√m
m=6
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Single Question)28videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Multiple Question)11videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.318videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises1316videos
CONIC SECTIONS
- BOOK - CENGAGECHAPTER - LIMITS AND DERIVATIVESEXERCISE - Solved Examples And Exercises320videos
LIMITS AND DERIVATIVES
Similar Questions
Knowledge Check
- Question 1 - Select One
If the vectors 2ˆi−3ˆj+4ˆkandˆi+2ˆj−ˆkandmˆi−ˆj+2ˆk are coplanar, then the value of m is
A58B85C−74D23 - Question 2 - Select One
If the vectors 2ˆi−3ˆj+4ˆkandˆi+2ˆj−ˆkandmˆi−ˆj+2ˆk are coplanar, then the value of m is
A58B85C−74D23 - Question 3 - Select One
The velociies of A and B are →vA=2ˆi+4ˆjand→vB=3ˆi−7ˆj , velocity of B as observed by A is
A5ˆi−3ˆjBˆi−11ˆjC−ˆi+11ˆjD2ˆi−3ˆj
What is the value of linear velocity →v if →ω=3ˆi−4ˆj+ˆk and →r=5ˆi−6ˆj+6ˆk ?
View SolutionFind unit vector in direction of friction force acting on block
→vp=7ˆi−2ˆj,→vB=3ˆi+ˆj
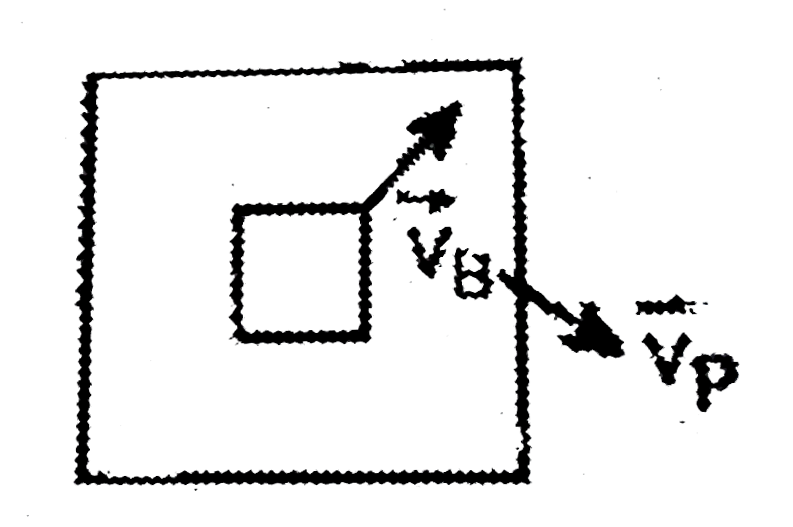 View Solution
View SolutionThe velocity (in m/s) of an object changes from →v1=10ˆi+4ˆj+2ˆkto→v2=4ˆi+2ˆj+3ˆk in 5 second. Find the magnitude of average acceleration.
View SolutionLet →uand→v be unit vectors such that →u×→v+→u=→wand→w×→u=→v . Find the value of [→u→v→w]
View SolutionLet →a=2ˆi−ˆj+2ˆkand→b=ˆi+2ˆj−ˆk. Let a vector →v be in the plane containing →aand→b. If →v is perpendicular to the vector 3ˆi+2ˆj−ˆk and its projection on →a is 19 units, then |2→v|2 is equal to _________.
View Solution

