BC யின் மையப்புள்ளி D மற்றும் AE ⊥BC BC =a ,AC =b ,AB =c ED =x ,AD =p மற்றும் AE =h எனில் b2+c2=2p2+a22 என நிரூபிக்க ?
Step by step video & image solution for BC யின் மையப்புள்ளி D மற்றும் AE _|_BC BC =a ,AC =b ,AB =c ED =x ,AD =p மற்றும் AE =h எனில் b^2+c^2=2 p^2+a^2 /2 என நிரூபிக்க ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
பின்வரும் முற்றொருமைகளை நிரூபிக்கவும். cotθ+tanθ=secθcosecθ
View SolutionProve that identities: ∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣=(ab+bc+ac)3
View SolutionProve |[-bc, b^2+bc, c^2+bc] , [a^2+ac, -ac, c^2+ac] , [a^2+ab, b^2+ab, -ab]|=(ab+bc+ca)^2
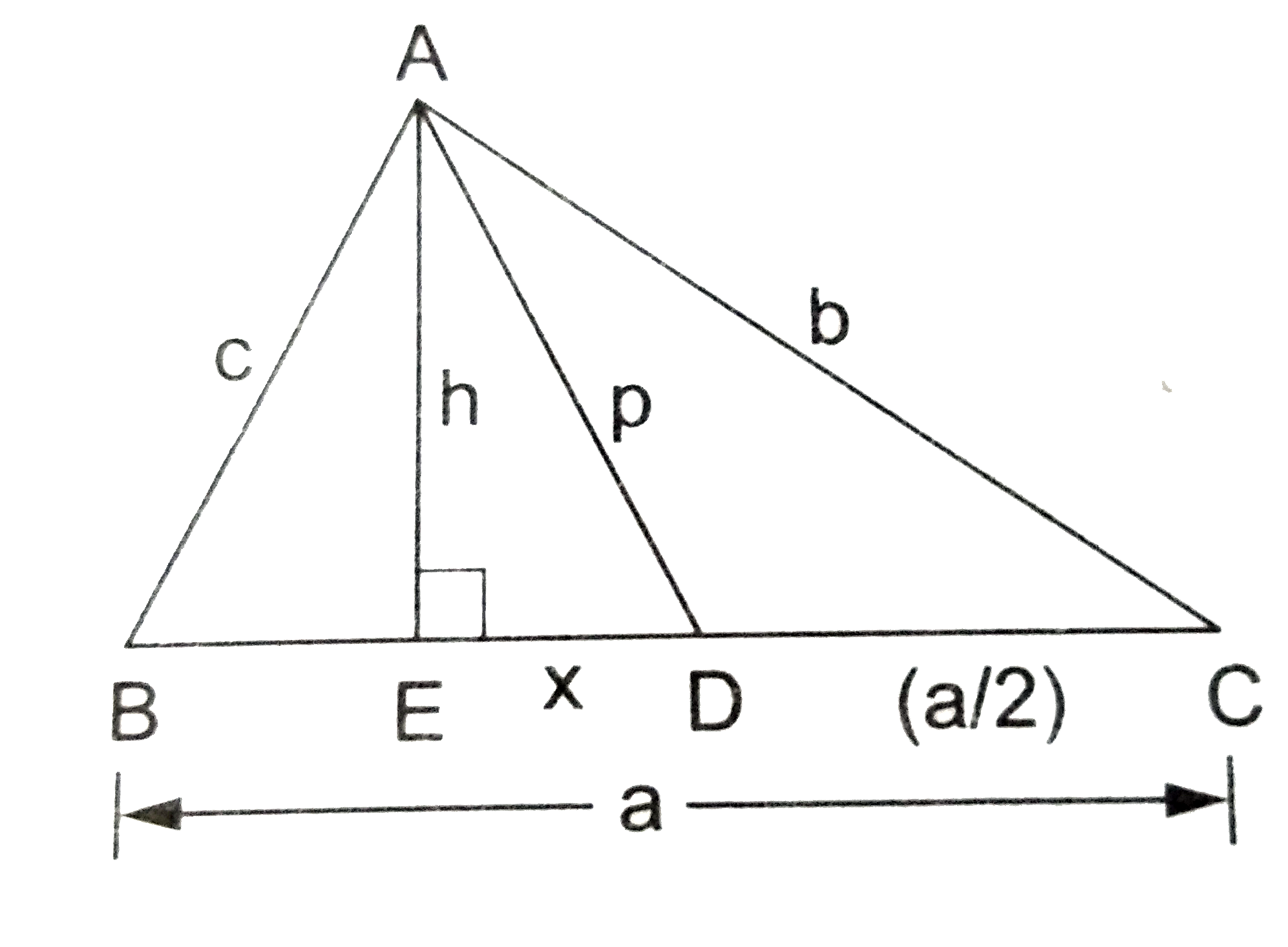
View SolutionIn the given figure, D is the midpoint of side BC and AE⊥BC. If BC=a,AC=b,AB=c,ED=xAD=pandAE=h prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii) (b2+c2)=2p2+12a2
(iv)(b2−c2)=2ax.
View Solutionयदि a,b,c में से कोई शून्य नहीं है तो दिखाएँ कि
Δ=∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣=(bc+ca+ab)3
View Solutionसिद्ध कीजिए कि:
∣∣∣ad+bcbd−acac−bdad+bc∣∣∣=(a2+b2)(c2+d2).
View Solutionprove that, ∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac −acc2+aca2+abb2+ab −ab∣∣ ∣ ∣∣=(ab+bc+ca)3
View SolutionD is the mid point of side BC and AE⊥BC. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii)b2+c2=2p2+a22
View Solutionপ্রমান করো যে,
∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac −acc2+aca2+abb2+ab −ab∣∣ ∣ ∣∣=(ab+bc+ca)3
View SolutionIn ΔABC, with ∠B=90∘, BC=6 cm and AB=8 cm, D is a point on AC such that AD=2 cm and E is the midpoint of AB. Join D to E and extend it to meet at F. Find BF.
View SolutionBC யின் மையப்புள்ளி D மற்றும் AE ⊥BC BC =a ,AC =b ,AB =c ED =x ,AD =p மற்றும் AE =h எனில் b2=p2 +ax+ a24 என நிரூபிக்க ?
View SolutionBC யின் மையப்புள்ளி D மற்றும் AE ⊥BC BC =a ,AC =b ,AB =c ED =x ,AD =p மற்றும் AE =h எனில் c2=p2_ax+a24 என நிரூபிக்க ?
View SolutionProve that identities: ∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣=(ab+bc+ac)3
View Solutionयदि सदिश (−bc,b2+bc,c2+bc),(a2+ac,−ac,c2+ac) व (a2+ab,b2+ab,−ab) समतलीय हैं, जहाँ a, b व c कोई भी शून्य नहीं है, तो
View SolutionUsing the properties of determinants show that : ∣∣ ∣ ∣∣⎡⎢⎣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab⎤⎥⎦∣∣ ∣ ∣∣=(ab+bc+ca)3
View Solution
