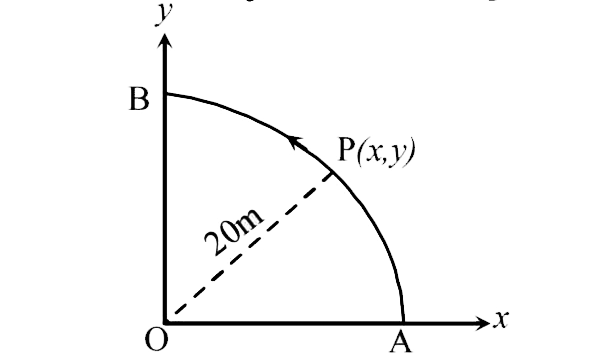
A point P moves in a counter clock wise direction on a circular path as shown in fig. The movement of 'P' is such that it sweeps out a length S=t3+5, where 'S' is in metres and 't' is in seconds. The radius of the path is 20m. The acceleration of 'P' when t=2s is nearly.

S=t3+5⇒v=dSdt=3t2
For t=2s,v=3×4=12ms−1
Tangential acceleration, at=dvdt=6t
For t2s,at=12ms−2
Centripetal acceleration
ac=v2r=14420=7.2ms−2
net acceleration =√a2t+a2c≈14ms−2
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EVALUATE YOURSELF - 1
11 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EVALUATE YOURSELF - 2
11 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
Similar Questions
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of P when t = 2 s is nearly
View SolutionA point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P ' is such that it sweeps out a length s=t3+5 where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of ' P ' when t = 2 s is nearly:

View Solution
Knowledge Check
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of P when t = 2 s is nearly
 A14m/s2B13m/s2C12m/s2D7.2m/s2
A14m/s2B13m/s2C12m/s2D7.2m/s2A point P moves in counter clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length s=t2+5, wheres is in metres and t is in seconds. The radius of the path is 20m. The acceleration of 'P' when t=5√310 seconds is nearly:
 A2m/s2B1.5m/s2C2.5m/s2D3m/s2
A2m/s2B1.5m/s2C2.5m/s2D3m/s2A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P ' is such that it sweeps out a length s=t3+5 where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of ' P ' when t = 2 s is nearly:
 A13m/s2B12m/s2C7.2m/s2D14m/s2
A13m/s2B12m/s2C7.2m/s2D14m/s2
A point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5 where s is in the metre and t is in seconds. The radius of the path is 27 m. The acceleration of P when t= 3 s is _________ m/s2. (Take √13=3.6)
View SolutionA point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5 where s is in the metre and t is in seconds. The radius of the path is 27 m. The acceleration of P when t= 3 s is _________ m/s2. (Take √13=3.6)

View SolutionA point P moves in counter-clockwise direction on figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in metre and t is in second. The radius of the pathh is 20 m. the acceleration of P when t=2s is nearly
View SolutionA point p moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length s=t3+5 , where s is in metres and t is in seconds . The radius of the path is 20m . The acceleration of 'P' when t=2s is nearly .
View SolutionA point p moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length s=t3+5 , where s is in metres and t is in seconds . The radius of the path is 20m . The acceleration of 'P' when t=2s is nearly .

View Solution
