Two identical blocks each of mass ''M'' are tied to the ends of a string and the string is laid over a smooth fixed pulley. Initially the masses are held at rest at the same level. What fraction of mass must be removed from one block and added to the other, so that it has an acceleration of 1/5th of the acceleration due to gravity
1/10
2.15
3.25
4.120
The correct Answer is:B
F=ma,a=(m1−m2m1+m2)g
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (C.W)(LAW OF CONSERVATION OF MOMENTUM)
4 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (C.W)(EQUILIBRIUM OF A PARTICLE)
3 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (C.W)(IMPULSE)
2 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
Similar Questions
Two blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
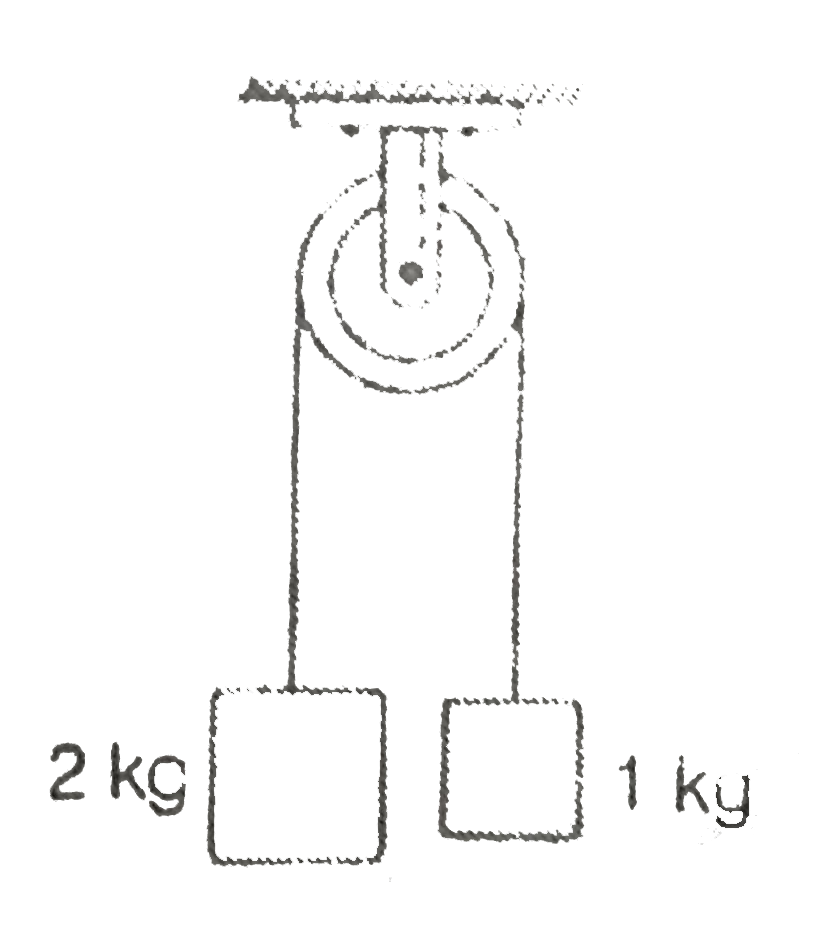
View SolutionTwo blocks of masses 2 kg and 1 kg respectively are tied to the ends of a string which passes over a light frictionless pulley . The masses are held at rest at the same horizontal level and then released . The distance traversed by centre of mass in 2 s is ( g = 10 m/s2)
View Solution
Knowledge Check
Two masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
Ag, vertically downwardsBg5, vertically downwardsCg25, vertically downwardsDzeroTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(m−m)gBmgC2mgD(mM)mg
Two blocks of masses 2 kg and 1 kg respectively are tied to the ends of a string which passes over a light frictionless pulley . The masses are held at rest at the same horizontal level and then released . The distance traversed by centre of mass in 2 s is ( g = 10 m/s2)

View SolutionTwo masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionTwo blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
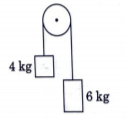
View SolutionTwo bodies of mass 4 kg and tied to the ends of a massless string. the string passes over a pully which is frictionless (see figure). the acceleration of the system in terms of acceleration due to gravity (g) is:
View SolutionTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is

View Solution
