Three bodies of equal masses are placed at (0,0) ,(a,0) and (a2.a√32) . Find out the cordinates of centre of mass .
(a2,a√36)
(a,a2)
(√3a6,a)
(a2,a2)
The correct Answer is:A
To find the coordinates of the center of mass of three bodies placed at the given coordinates, we can follow these steps:
Step 1: Identify the coordinates and masses
We have three bodies with equal masses m located at the following coordinates:
1. Body 1: (0,0)
2. Body 2: (a,0)
3. Body 3: (a2,a√32)
Step 2: Use the center of mass formula
The formula for the center of mass (xcm,ycm) for a system of particles is given by:
xcm=∑mixi∑mi
ycm=∑miyi∑mi
Since all masses are equal, we can denote the mass of each body as m.
Step 3: Calculate xcm
Substituting the coordinates into the formula for xcm:
xcm=m⋅0+m⋅a+m⋅a2m+m+m
=0+a+a23m
=a+a23
=2a2+a23=3a23=a2
Step 4: Calculate ycm
Now, substituting the coordinates into the formula for ycm:
ycm=m⋅0+m⋅0+m⋅a√32m+m+m
=0+0+a√323m
=a√323=a√36
Step 5: Final coordinates of the center of mass
Thus, the coordinates of the center of mass are:
(a2,a√36)
Summary
The center of mass of the three bodies is located at:
(a2,a√36)
We have three bodies with equal masses m located at the following coordinates:
1. Body 1: (0,0)
2. Body 2: (a,0)
3. Body 3: (a2,a√32)
The formula for the center of mass (xcm,ycm) for a system of particles is given by:
xcm=∑mixi∑mi
ycm=∑miyi∑mi
Since all masses are equal, we can denote the mass of each body as m.
Substituting the coordinates into the formula for xcm:
xcm=m⋅0+m⋅a+m⋅a2m+m+m
=0+a+a23m
=a+a23
=2a2+a23=3a23=a2
Now, substituting the coordinates into the formula for ycm:
ycm=m⋅0+m⋅0+m⋅a√32m+m+m
=0+0+a√323m
=a√323=a√36
Thus, the coordinates of the center of mass are:
(a2,a√36)
The center of mass of the three bodies is located at:
(a2,a√36)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 411videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 210videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)19videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Four particles of masses m,2m,3m,4m are placed at corners of a square of side 'a' as shown in fig. Find out coordinateds of centre of mass.
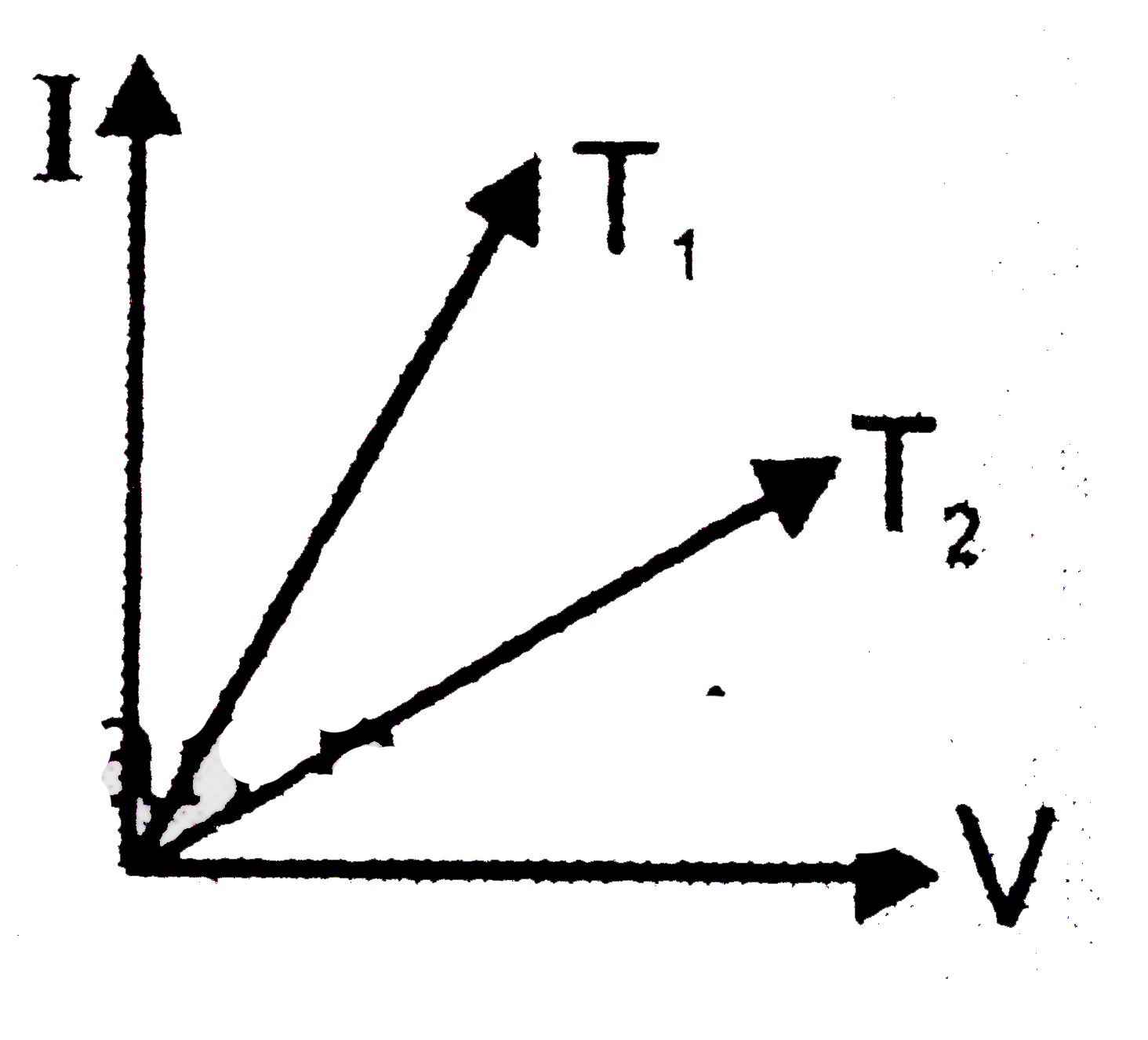 View Solution
View SolutionThree point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
View Solution
Knowledge Check
- Question 1 - Select One
Vertics of a triangle ABC are the points (0,0),(a,0) and (a2,a√32). Its incentre is the point
A(3a4,√3a4)B(a2,a√36)C(a6,a√32)D(a3,a√32) - Question 2 - Select One
Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
A2m from 1 kgB2m from 2 kgC1m from 1 kgDnone of these
Fig. shown a three particle system with masses m1=3.0kg,m2=4.0kg and m3=8.0kg. The scales on the axes are set by xs=2.0m and ys=2.0m. What are the co-ordinates of centre if mass ? If m3 is gradually increased, does the centre of mass of the system shift towards or away from that particle or does it remain stationary ?
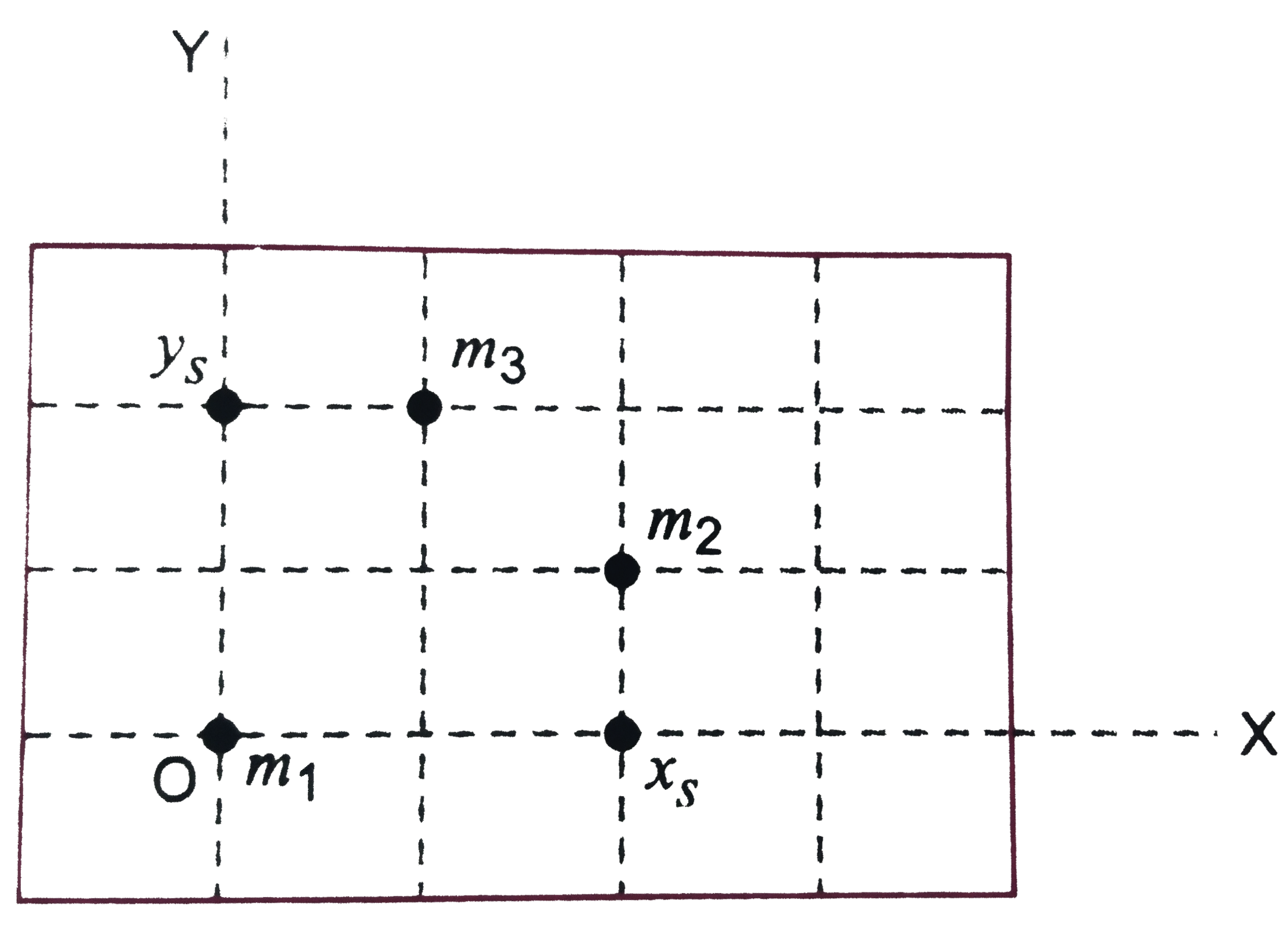 View Solution
View SolutionIf three vertices of a rectangle or (0,0), (2,0)and(0, 3), find the coordinates of the fourth vertex.
View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionTwo particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.
 View Solution
View SolutionThree laminar bojects of uniform density a square, a disc and an equilateral triagle are placed as shown fig. find the coordinates of centre of mass of the three bodies.
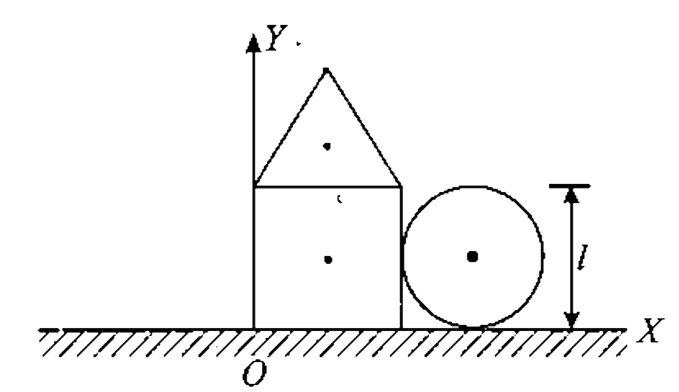 View Solution
View SolutionThree point masses of 1kg,2kgand3kg lie at (1,2),(0,−1)and(2,−3) respectively. Calculate the co-ordinates of the centre of mass of the system.
View Solution

