The angular velocity of a rotating disc decreases linearly with angular displacement from 60 rev/min to zero during 10 rev . Determine the angular velocity of the disc 3 sec after it begins to slow down
20π10 rad/sec
17π10 rad/sec
(7π)3 rad/sec
10π3 rad/sec
The correct Answer is:B
To solve the problem, we need to determine the angular velocity of a rotating disc that decreases linearly from 60 revolutions per minute (rev/min) to 0 over a displacement of 10 revolutions. We will find the angular velocity after 3 seconds of deceleration.
1. Convert Initial Angular Velocity to Radians per Second:
- The initial angular velocity (ω_initial) is given as 60 rev/min.
- To convert this to radians per second, we use the conversion factor 2π radians per revolution and 60 seconds per minute:
ωinitial=60rev/min×2πradians1rev×1min60s=2πradians/s
2. Determine Angular Displacement in Radians:
- The angular displacement (θ) is given as 10 revolutions.
- Converting this to radians:
θ=10rev×2πradians/rev=20πradians
3. Calculate Angular Acceleration:
- Since the angular velocity decreases linearly, we can use the equation:
ω2final=ω2initial+2αθ
- Here, ωfinal=0 (the disc stops), ωinitial=2π, and θ=20π.
- Plugging in the values:
0=(2π)2+2α(20π)
- Simplifying gives:
0=4π2+40πα
- Rearranging for α:
40πα=−4π2⟹α=−4π240π=−π10radians/s2
4. Find Angular Velocity After 3 Seconds:
- We use the angular velocity equation:
ωfinal=ωinitial+αt
- Here, t=3s, ωinitial=2π, and α=−π10:
ωfinal=2π+(−π10)(3)
- Simplifying:
ωfinal=2π−3π10=20π10−3π10=17π10radians/s
Final Answer:
The angular velocity of the disc after 3 seconds is 17π10radians/s.
- The initial angular velocity (ω_initial) is given as 60 rev/min.
- To convert this to radians per second, we use the conversion factor 2π radians per revolution and 60 seconds per minute:
ωinitial=60rev/min×2πradians1rev×1min60s=2πradians/s
- The angular displacement (θ) is given as 10 revolutions.
- Converting this to radians:
θ=10rev×2πradians/rev=20πradians
- Since the angular velocity decreases linearly, we can use the equation:
ω2final=ω2initial+2αθ
- Here, ωfinal=0 (the disc stops), ωinitial=2π, and θ=20π.
- Plugging in the values:
0=(2π)2+2α(20π)
- Simplifying gives:
0=4π2+40πα
- Rearranging for α:
40πα=−4π2⟹α=−4π240π=−π10radians/s2
- We use the angular velocity equation:
ωfinal=ωinitial+αt
- Here, t=3s, ωinitial=2π, and α=−π10:
ωfinal=2π+(−π10)(3)
- Simplifying:
ωfinal=2π−3π10=20π10−3π10=17π10radians/s
The angular velocity of the disc after 3 seconds is 17π10radians/s.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 411videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 210videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)19videos
THERMAL PROPERTIES OF MATTER
Similar Questions
The square of the angular velcoity ω of a certain wheel increases linearly with the angular displacement during 100rev of the wheel's motion as shown. Compute the time t required for the increase.
 View Solution
View Solution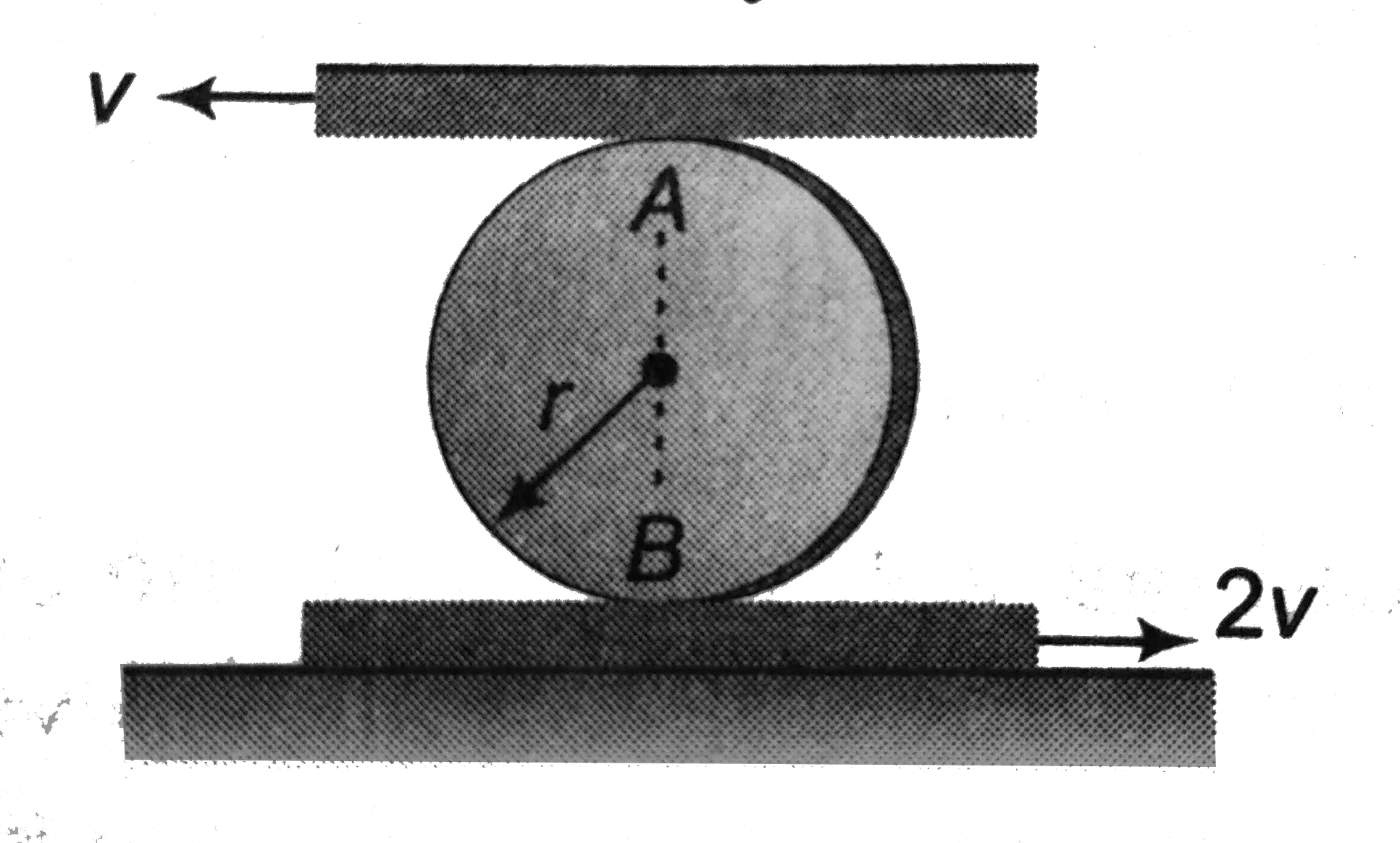
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.View Solution
Knowledge Check
- Question 1 - Select One
An ant is sitting at the edge of a rotating disc. If the ant reaches the other end, after moving along the diameter, the angular velocity of the disc will:-
Aremain constantBfirst decreases and then increasesCfirst increases, then decreaseDIincrease continuously - Question 2 - Select One
A heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
AincreaseBdecreaseCbecomes zeroDremain unchanged - Question 3 - Select One
A disc rotates with angular velocity ω and kinetic energy E. Then its angular momentum
AIωBL=EωCL=2EωDL=ωE
The angular velocity of circular disc of radius 2cm is 20 rad s−1. Calculate the linear velocity of the disc.
View SolutionA disc starts rotating with constant angular acceleration of πrads2 about a fixed axis perpendicular to its plane and through its centre .
(a) Find the angular velocity of the disc after 4s .
(b) Find the angular displacement of the disc after 4 s and
(c ) Find number d of turns accomplished by the disc in 4 s .View SolutionFind the angular velocity of a body rotating wilth an acceleration of 2revs2 as it completes the 5th revolution after the start
View SolutionThe speed of a body moving in a circle of radius 15 cm changes from 180rev/min→600rev/minin11s . Then the angular acceleration of the body will be
View SolutionA basketball player is balancing a spinning basketball on the tip of his finger. The angular velocity of the ball slows down from 18.5 to 14.1 rad/s. During the slow-down, the angular displacement is 85.1 rad. Determine the time it takes for the ball to slow down.
View Solution

