A meter scale weighs 50 gms and carries 20 gm at one end , the scale balances when it is suspende at a distance x cm from other end . Then x I equal to
35.7 cm
64.3 cm
14.3 cm
50 cm
The correct Answer is:B
To solve the problem, we need to analyze the forces and torques acting on the meter scale. Let's break down the steps:
1. Identify the Given Information:
- Weight of the meter scale, Ws=50g=0.05kg (since 1 g = 0.001 kg)
- Weight of the mass at one end, Wm=20g=0.02kg
- Length of the scale, L=100cm
2. Determine the Center of Mass:
- The center of mass of the meter scale is located at its midpoint, which is at 50cm from either end.
3. Set Up the Torque Equation:
- The scale is balanced when suspended at a distance x from the end opposite to the mass.
- The torque due to the weight of the scale about the pivot point (suspension point) is calculated as follows:
- Torque due to the weight of the scale (anticlockwise):
τs=Ws⋅ds=0.05⋅g⋅(x−50)
- Torque due to the weight of the mass (clockwise):
τm=Wm⋅dm=0.02⋅g⋅(100−x)
4. Set the Net Torque to Zero:
- For the scale to be in equilibrium, the net torque must be zero:
τs−τm=0
- Substituting the torque equations:
0.05⋅g⋅(x−50)−0.02⋅g⋅(100−x)=0
- Cancel g from both sides:
0.05(x−50)=0.02(100−x)
5. Simplify the Equation:
- Expanding both sides:
0.05x−2.5=2−0.02x
- Rearranging the equation:
0.05x+0.02x=2+2.5
0.07x=4.5
6. Solve for x:
- Dividing both sides by 0.07:
x=4.50.07≈64.2857cm
- Rounding to two decimal places gives:
x≈64.29cm
Final Answer:
The value of x is approximately 64.3cm.
---
- Weight of the meter scale, Ws=50g=0.05kg (since 1 g = 0.001 kg)
- Weight of the mass at one end, Wm=20g=0.02kg
- Length of the scale, L=100cm
- The center of mass of the meter scale is located at its midpoint, which is at 50cm from either end.
- The scale is balanced when suspended at a distance x from the end opposite to the mass.
- The torque due to the weight of the scale about the pivot point (suspension point) is calculated as follows:
- Torque due to the weight of the scale (anticlockwise):
τs=Ws⋅ds=0.05⋅g⋅(x−50)
- Torque due to the weight of the mass (clockwise):
τm=Wm⋅dm=0.02⋅g⋅(100−x)
- For the scale to be in equilibrium, the net torque must be zero:
τs−τm=0
- Substituting the torque equations:
0.05⋅g⋅(x−50)−0.02⋅g⋅(100−x)=0
- Cancel g from both sides:
0.05(x−50)=0.02(100−x)
- Expanding both sides:
0.05x−2.5=2−0.02x
- Rearranging the equation:
0.05x+0.02x=2+2.5
0.07x=4.5
- Dividing both sides by 0.07:
x=4.50.07≈64.2857cm
- Rounding to two decimal places gives:
x≈64.29cm
The value of x is approximately 64.3cm.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - II (C.W)60videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - II (H.W)60videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - I (C.W)63videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)19videos
THERMAL PROPERTIES OF MATTER
Similar Questions
What is the acceleration of pulse when it is at x distance from bottom end?
View SolutionA balance similar to a Roman steel yard is constructed such that the length of the scale on the beam of the balance is 50 cm and the least count on the scale is 1 mm. The zero mark of the scale is at a distance of 15 cm from the point of suspension of the balance. The hook that is used to attach the loads and the centre of gravity of the beam are at distance 8 cm and 5 cm, respectively, from its fulcrum. If the weight of the rider of the balance is 50 gf, find the weight of the beam, the maximum load that can be measured using the balance and its least count.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform bar RS weighs 100 g and is 80 cm long. From the end R, two masses 50 g and 100 g are hung from the bar at a distance of 10 cm and 60 cm respectively. If the bar is to remain horizontal when balanced on a knifeedge, its position is
A42 cm from SB38 cm from RC38 cm from GD42 cm from R - Question 2 - Select One
An uniform metre scale of weight 50g is balanced at 60cm mark, when a weight of 15g is suspended at 10cm mark. Where must a weight 100g be suspended to balance metre scale.
A72.5cmB70cmC71.5cmD74.5cm - Question 3 - Select One
A meter scale is balanced at its mid point if a 20N weight is balanced at 20 cm mark and a 30 N weight hanged at x cm mark. Calculate the value of x.
A20 cmB70 cmC30 cmD80 cm
When two known resistance R and S are connected in the left and right gaps of a meter bridge, the balance point is found at a distance l1 from the zero end of the meter bridge wire. An unknown resistance X is now connected in parallel to the resistance S and the balance point is found at a distance l2 from the zero end of the meter bridge wire,
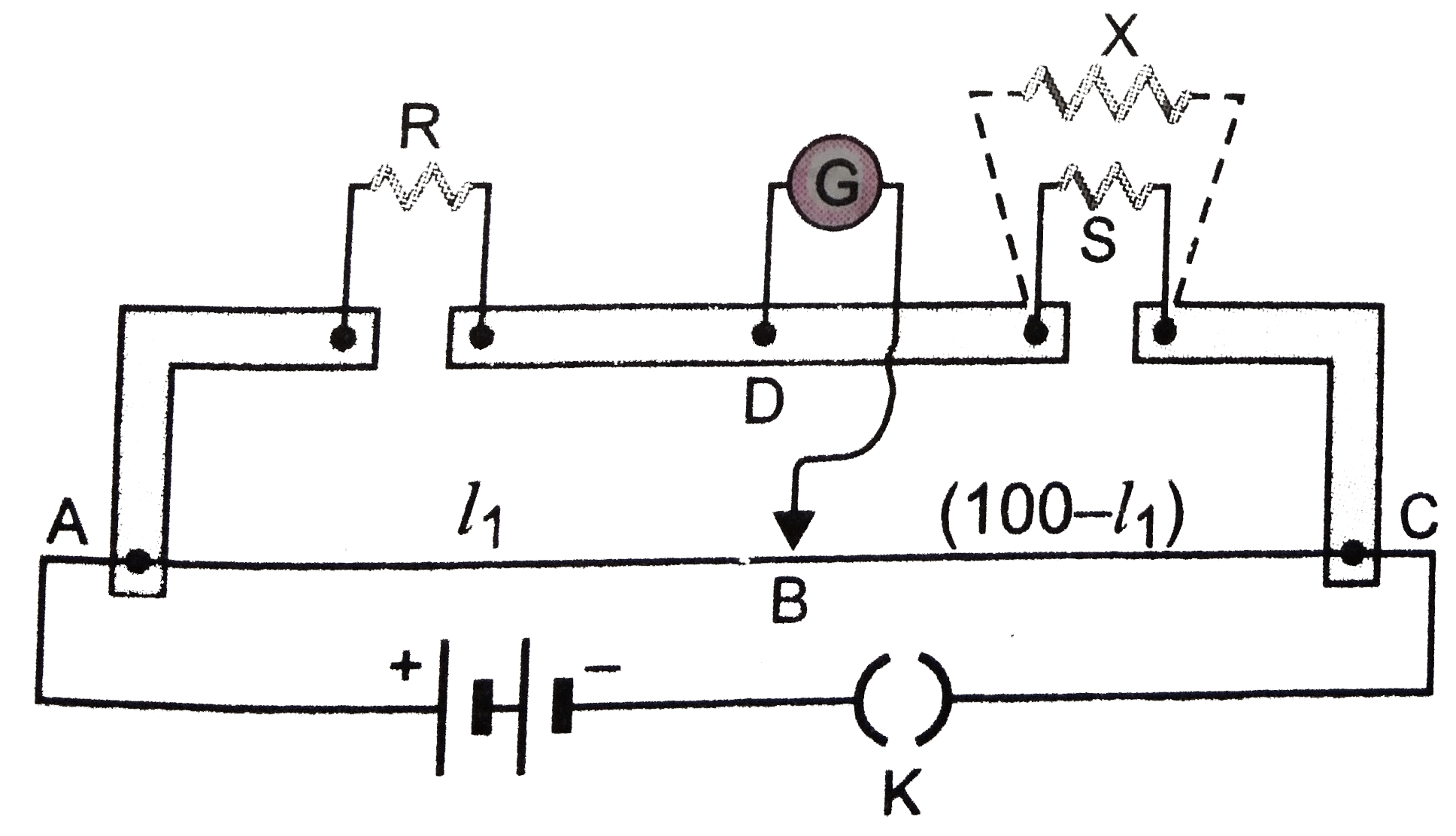
Obtain a formula for X in terms of l1,l2 and S.View SolutionA uniform metre scale 1 m long is suspended at 50 cm division. A known weight of 160 gwt is tied at 80 cm division and the scale is balanced by a weight of 240 gwt tied to the scale at a certain distance from the point of suspension on the opposite side. Calculate this distance.
View SolutionA metal rod of length 50cm having mass 2kg is supported on two edges placed 10cm from each end. A 3kg load is suspended at 20cm from one end. Find the reactions at the edges (take g=10m/s2)
View SolutionIn order to balance a see-saw of total length 10.0m, two kids weighing 20 kg and 40 kg are sitting at an end and at a distance x from the fulcrum at the centre, respectively The value x (in cm) is
View SolutionIn a meter bridge experiment, null point is obtained at 20cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y will be at.
View Solution

