In order to balance a see-saw of total length 10.0m, two kids weighing 20 kg and 40 kg are sitting at an end and at a distance x from the fulcrum at the centre, respectively The value x (in cm) is
125
250
450
350
To solve the problem of balancing the seesaw, we need to apply the principle of moments (torque). Here’s a step-by-step solution:
Step 1: Understand the Setup
The seesaw has a total length of 10.0 m, which means the distance from the fulcrum (the center) to each end is 5.0 m. One child weighs 20 kg and is sitting at one end (5.0 m from the fulcrum), while the other child weighs 40 kg and is sitting at a distance x from the fulcrum.
Step 2: Write the Torque Equation
For the seesaw to be balanced, the clockwise moments must equal the anti-clockwise moments. The torque (moment) is calculated as the product of the force and the distance from the fulcrum.
- The torque due to the 20 kg child (let's call this WA):
WA=20kg×g
The distance from the fulcrum is 5.0 m, so the torque is:
TorqueA=WA×5.0
- The torque due to the 40 kg child (let's call this WB):
WB=40kg×g
The distance from the fulcrum is x, so the torque is:
TorqueB=WB×x
Step 3: Set Up the Equation
Since the seesaw is in equilibrium:
TorqueA=TorqueB
Substituting the expressions for torque:
(20×g)×5.0=(40×g)×x
Step 4: Simplify the Equation
We can cancel g from both sides:
20×5.0=40×x
This simplifies to:
100=40x
Step 5: Solve for x
Now, divide both sides by 40:
x=10040=2.5m
Step 6: Convert to Centimeters
Since the question asks for x in centimeters:
x=2.5m×100=250cm
Final Answer
Thus, the value of x is 250 cm.
---
The seesaw has a total length of 10.0 m, which means the distance from the fulcrum (the center) to each end is 5.0 m. One child weighs 20 kg and is sitting at one end (5.0 m from the fulcrum), while the other child weighs 40 kg and is sitting at a distance x from the fulcrum.
For the seesaw to be balanced, the clockwise moments must equal the anti-clockwise moments. The torque (moment) is calculated as the product of the force and the distance from the fulcrum.
WA=20kg×g
The distance from the fulcrum is 5.0 m, so the torque is:
TorqueA=WA×5.0
WB=40kg×g
The distance from the fulcrum is x, so the torque is:
TorqueB=WB×x
Since the seesaw is in equilibrium:
TorqueA=TorqueB
Substituting the expressions for torque:
(20×g)×5.0=(40×g)×x
We can cancel g from both sides:
20×5.0=40×x
This simplifies to:
100=40x
Now, divide both sides by 40:
x=10040=2.5m
Since the question asks for x in centimeters:
x=2.5m×100=250cm
Thus, the value of x is 250 cm.
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Two small kids weighing 10 g and 15 kg respectively are tyribg t balance a seesaw of total length 5.0 with the fulcrum at the centre. If one of the kids is sitting at an end where shold the other sit?
View SolutionTwo particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.
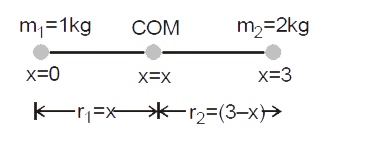
View Solution
Knowledge Check
6 m long see-saw remains horizontal when two children weighing 20 kg and 30 kg respectively sit at two ends. Where is the see-saw supported?
A3.6 m from 20 kgB2.6 m from 30 kgC4 m from 20 kgD4.2 m from 30 kgA steel bar AB of mass 10 kg and length 1 m is kept horizontal by supporting it at the two ends. Two weights of 4 kg and 6 kg are suspended from points of the bar at distances 30 cm and 80 cm respectively from the end A. The reaction at the end A is
A107.8 NB97.8 NC88.2 ND78.2 NThree children are sitting on a see-saw in such a way that is balances. A 20kg and a 30kg boy are on opposite sides at a distance of 2m from the pivot. It the third boy jumps off, thereby destroying balance, then the initial angular acceleration of the board is: (Neglect weight of board)
A0.01rads−2B1.0rads−2C10rads−2D100rads−2
Two children, weighing 30 kg and 15 kg sit on one side of a see-saw at a distance of 1m and 1.2 m respectively, from the fulcrum. A boy of 'M' kg sits on the other side of the see-saw at a distance of 1.2 m from the fulcrum, and the see saw is in equilibrium. Find M
View SolutionA meter scale weighs 50 gms and carries 20 gm at one end , the scale balances when it is suspende at a distance x cm from other end . Then x I equal to
View SolutionA uniform bar RS weighs 100 g and is 80 cm long. From the end R, two masses 50 g and 100 g are hung from the bar at a distance of 10 cm and 60 cm respectively. If the bar is to remain horizontal when balanced on a knifeedge, its position is
View SolutionAB is a straight line of length 150 cm. Two particles of masses 1 and 3 kg are placed at a distance of 15 cm from A and 50 cm from B respectively. The distance of the third particle of mass 2 kg from A, so that the C.G. of the system is at the middle point of AB is
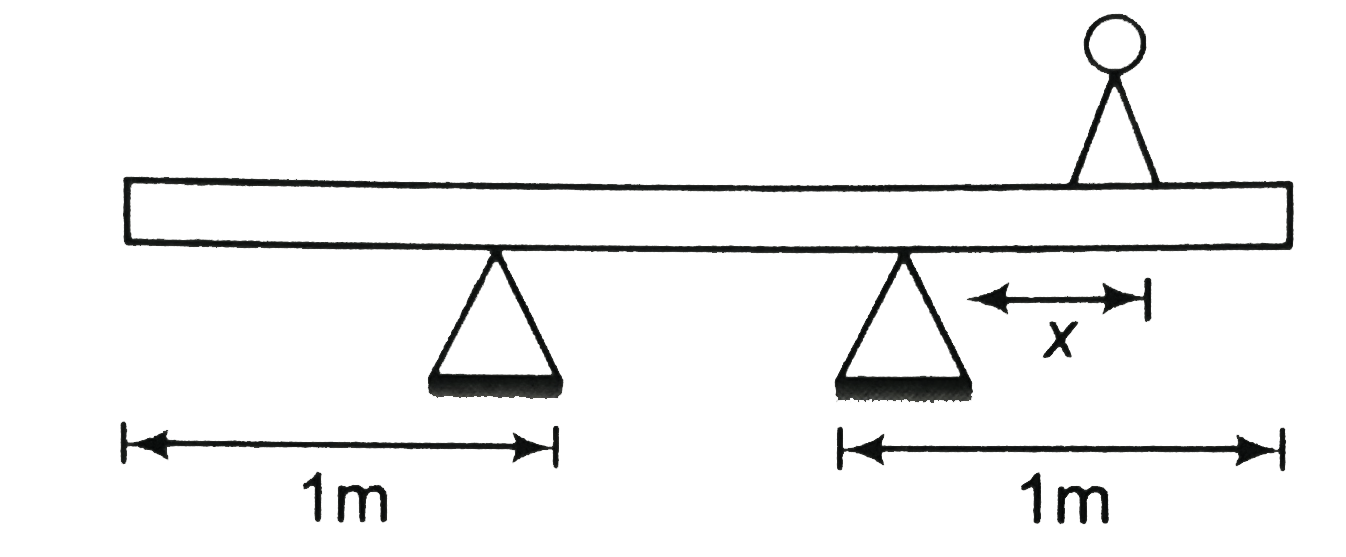
View SolutionA horizontal plank is 10.0m long with uniform density and mass 10kg .It rests on two supports which are placed 1.0m from each end as shown in the figure. A man of mass 80 kg can stand upto distance x on the plank without causing it to tip .The value of x is
View Solution
