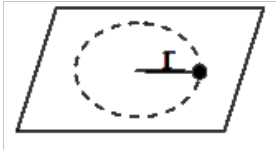
A small mass attached to a string rotates on frictionless table top as shown . If the tension is the string is increase by pulling the string causing the radius of the circular motion to decrease by a factor of 2 , the kinetic energy of the mass will

Remain constant
Increase by a factor of 2
Increase by a factor of 4
Decrease by a factor of 2
The correct Answer is:C
From the law of conservation of angular momentum . mvr=mvIr2⇒vI=2v
So , k1k2=12mv212mv2⇒k1k2=v2v2=v2(2v)2
⇒k1k2=14⇒k1=14k2k2=4k1
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - II (H.W)
60 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
A small mass attached to a string rotates on a frictionless table top as shown. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will
View SolutionA small body of mass m is tried to a string and revolved in a vertical circle of radius r. If the tension in the string at the highest point is mg, what is its speed there?
View Solution
Knowledge Check
A small mass attached to a string rotates on a frictionless table top as shown in Fig. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will
 Aremain constantBincrease by a factor of 2Cincrease by a factor of 4Ddecrease by a foctor of 2
Aremain constantBincrease by a factor of 2Cincrease by a factor of 4Ddecrease by a foctor of 2A particle of mass m is rotated in a vertical circle by means of a string . The differnce in the tensions in the string at the bottom and the top of the circle would be
A2 mgB3 mgC4mgD6 mgSpeed of transverse wave on string is v . If tension is increased by factor of 4 and radius of the string is increased by factor of 2, then the new wave speed will be :
A√2vBvC4vD2√2v
Speed of transverse wave on string is v . If tension is increased by factor of 4 and radius of the string is increased by factor of 2, then the new wave speed will be :
View SolutionSpeed of transverse wave on string is v . If tension is increased by factor of 4 and radius of the string is increased by factor of 2, then the new wave speed will be :
View SolutionA uniform sphere of weight W and radius 3 m is being held by a frictionless wall as shown in the figure. The tension in the string will be (length of the string is 2m):
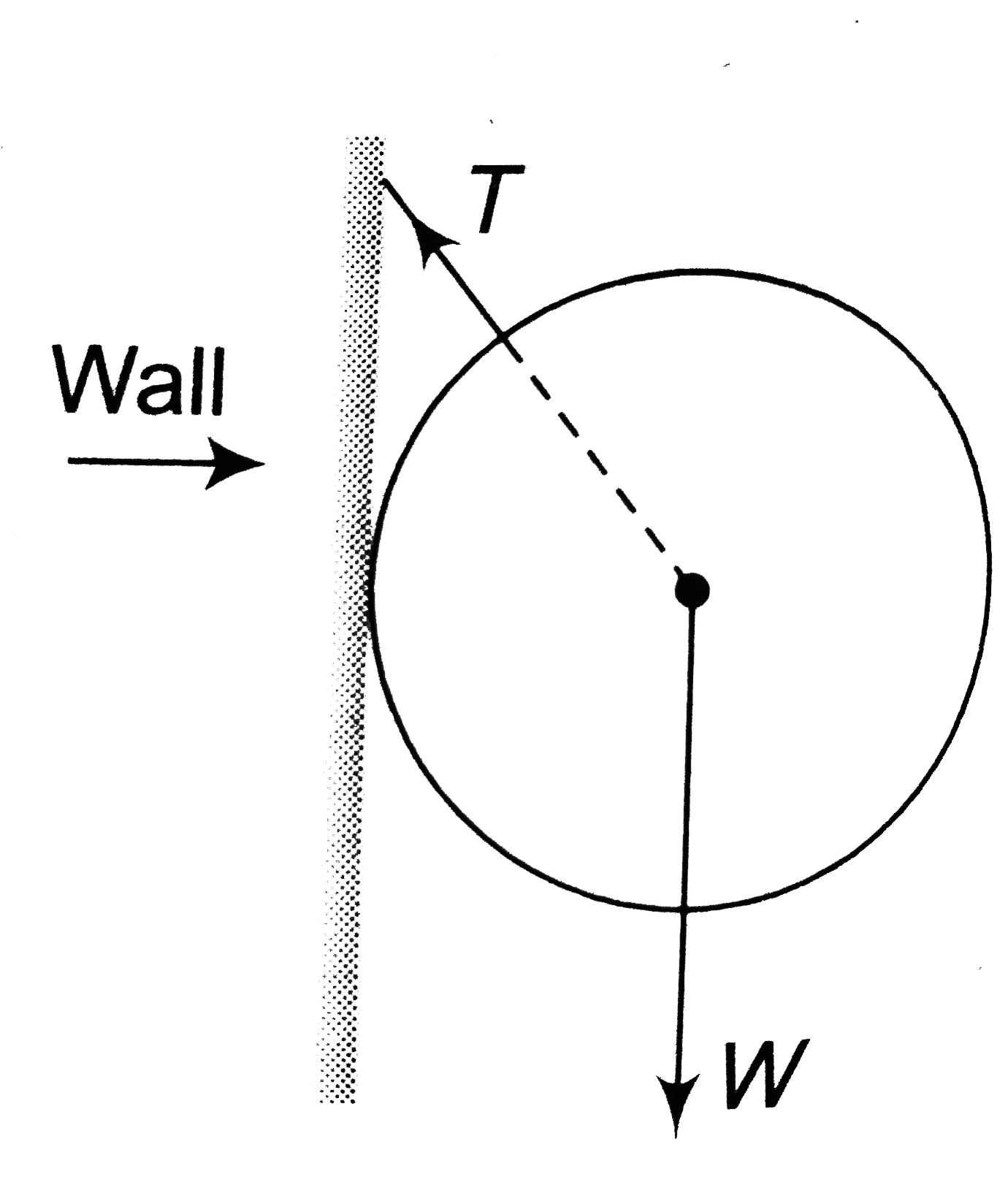
View SolutionA mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0, The mass is attached to a string which passes through a smooth hole in the plane as shown.
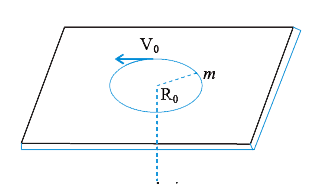
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy is :
View SolutionA mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
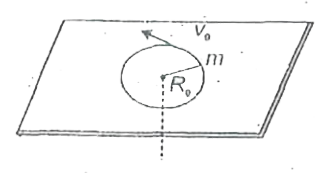
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy is
View Solution
