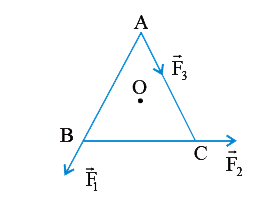
ABC is an equilateral triangle with O as its centre , ¯¯¯F1,¯¯¯F2and¯¯¯F3 represent three forces acting along the sides AB, BC and AC respectively . If the total torque about O is zero then the magnitude of ¯¯¯¯¯–––(F)3 is

¯¯¯F1+¯¯¯F2
¯¯¯F1−¯¯¯F2
¯¯¯F1+¯¯¯F22
2(¯¯¯F1+¯¯¯F2)
The correct Answer is:A
If we take clockwise torque
τ=τF1+τF2+τF3, O=F1r+F2r+F3r,F3=F1+F2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (H.W)
Explore 60 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
ABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

View SolutionABC is an equilateral with O as its centre →F1,→F2 and →F3 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of →F3 is :
View Solution
Knowledge Check
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
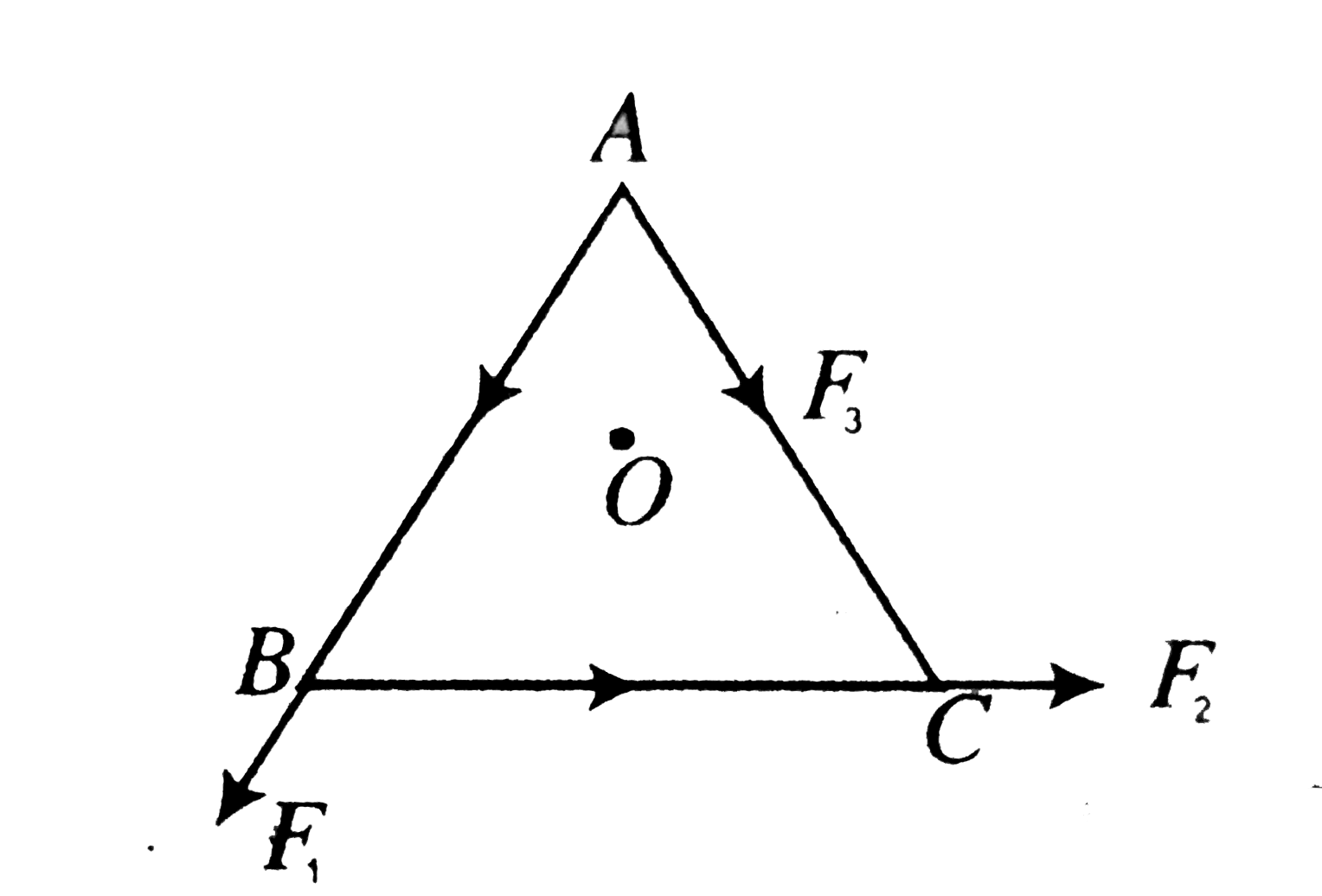 A2(F1+F2)BF1+F22CF1−F2DF1+F2
A2(F1+F2)BF1+F22CF1−F2DF1+F2O is the centre of an equilateral triangle ABC. F1,F2 and F3 are three forces acting along the sides AB, BC and AC as shown in the figure. What should be the magnitude of F3, so that the total torque about O is
 A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)
A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)ABC is an equilateral triangle. P and Q are two points on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯AC respectively such that ¯¯¯¯¯¯PQ∣∣¯¯¯¯¯¯BC. If ¯¯¯¯¯¯PQ=5cm, then area of ΔAPQ is :
A254 sq. cmB25√3 sq. cmC25√34 sq. cmD25√3 sq. cm
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?

View SolutionABC is an equilateral triangle of side ‘a'. Then ¯¯¯¯¯¯AB.¯¯¯¯¯¯BC+¯¯¯¯¯¯BC.¯¯¯¯¯¯CA+¯¯¯¯¯¯CA.¯¯¯¯¯¯AB=
View SolutionIf ¯¯¯E and ¯¯¯F are the complementary events of E and F respectively and if 0<P(F)<1, then
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC and O is any point in the plane of △ABC. Show that (1)¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF=¯0
View SolutionThree forces ¯¯¯¯F1,¯¯¯¯F2and¯¯¯¯F3 are simultaneously acting on a particle of mass 'm' and keep it in equilibrium. If ¯¯¯¯F1 force is reversed in direction only, the acceleration of the particle will be.
View Solution
