Transverse waves are produced in a stretched wire. Both ends of the string are fixed. Let us compare between second overtone mode (in numerator) and fifth harmonic, mode (in denominator).
match the following column-I with column-II

A

$a - r, b - p, c - r, d - s$

B

$a - q, b - p, c - s, d - s$

C

$a - r, b - s, c - q, d - p$

D

$a - s, b - p, c - r, d - p$

Video Solution

Text Solution

Verified by Experts

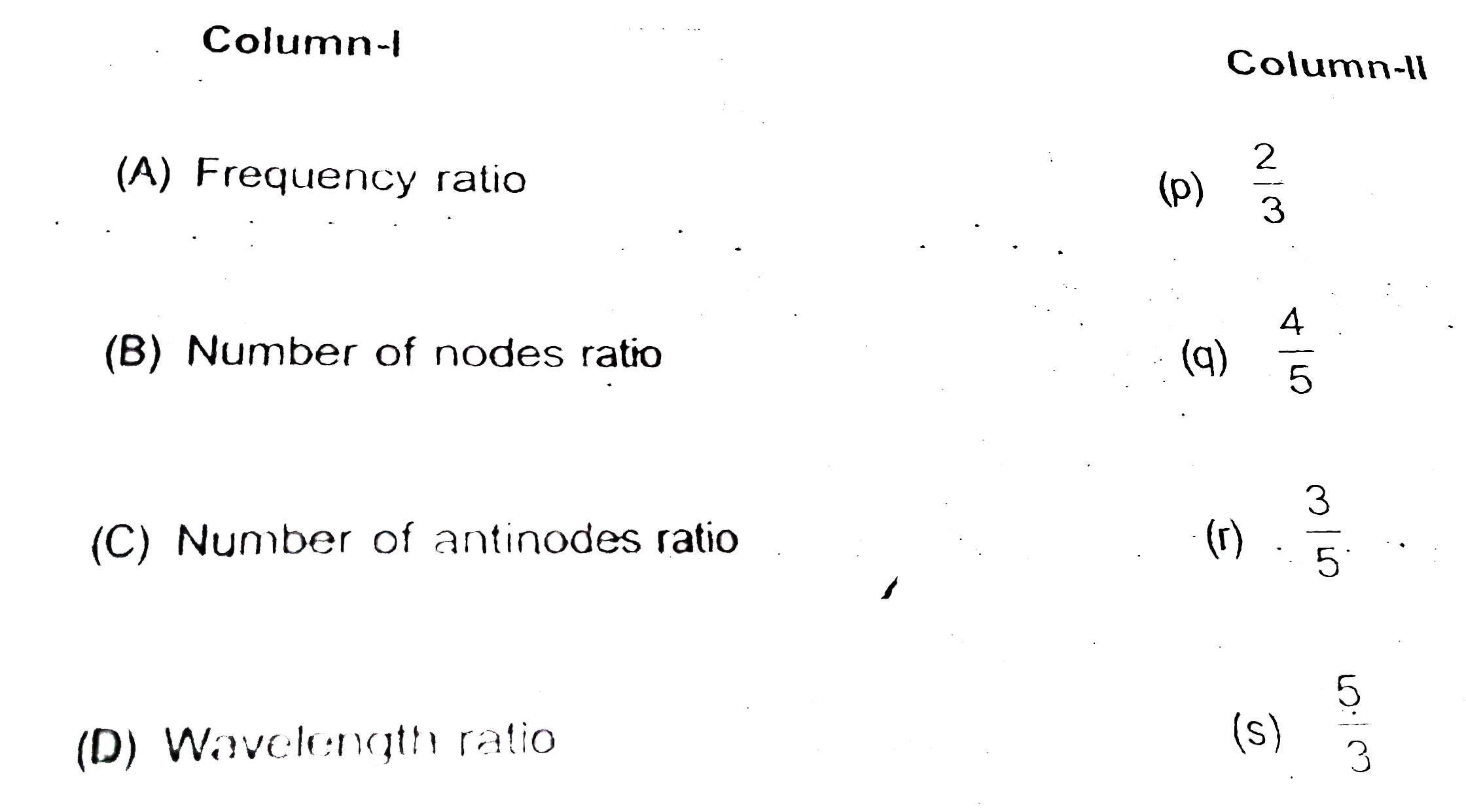
The correct Answer is:A

In second overtone number of antinodes is $3$ , nodes is $4$ and in fifth harmonic number of antinodes is $5$ and nodes is $6$ .

|

Updated on:21/07/2023

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A wire is stretched and fixed at two ends. Transverse stationary waves are formed in it. It oscillates in its third overtone mode. The equation of stationary wave is
$y = A sin k x cos ω t$
Choose the correct options.
AAmplitude of constituent waves is $\frac{A}{2}$
BThe wire oscillates in three loops
CThe length of the wire is $\frac{4 π}{k}$
DSpeed of stationary wave is $\frac{ω}{k}$
Question 2 - Select One
Stationary waves are produced in a length of wire fixed between two points . Compare the amplitudes at an antinode for the fundamental and the first overtone . Assume that the total energy of the initial waves is, on an average, equally divided between the two modes.
A $\frac{3}{\sqrt{2}}$
B $\frac{1}{\sqrt{2}}$
C $\frac{1}{2}$
D $\frac{1}{2 \sqrt{2}}$
Question 3 - Select One
Assertion: A wire is stretched and then fixed at two ends. It oscillates in its second overtone mode. There are total four nodes and three antinodes.
Reason: In second overtone mode, length of wire should be $l = \frac{3 λ}{2}$ , where $λ$ is wavelength.
AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
CIf Assertion is true, but the Reason is false.
DIf Assertion is false but the Reason is true.

NARAYNA-WAVES-Exercise-II (C.W)

Home
Ask Doubt
Profile