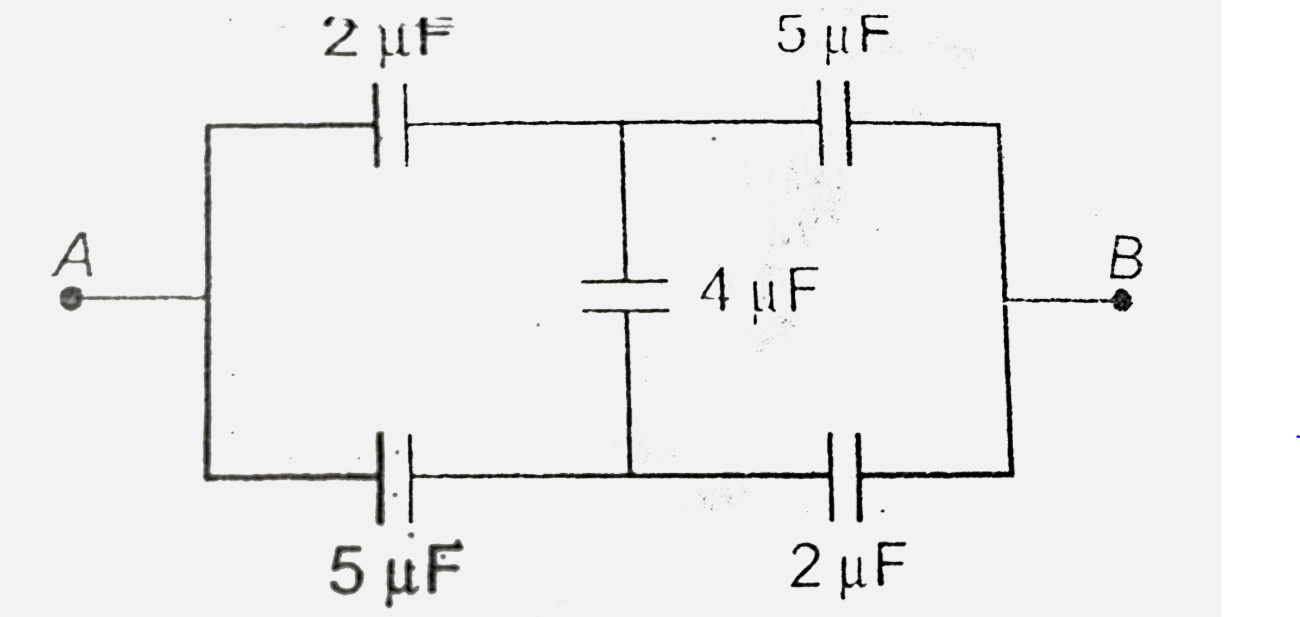
Find the effective capacitance between A and B of the arrangement shown ?


To find the effective capacitance between points A and B in the given arrangement of capacitors, we will follow these steps:
Step 1: Identify the Capacitors and Their Values
We have four capacitors:
- C1 = 3μF
- C2 = 6μF
- C3 = 4μF
- C4 = 12μF
Step 2: Determine the Configuration of Capacitors
From the arrangement, we can see that:
- Capacitors C1 and C2 are in series.
- Capacitors C3 and C4 are also in series.
Step 3: Calculate the Equivalent Capacitance of C1 and C2
For capacitors in series, the formula for equivalent capacitance (C') is given by:
1C′=1C1+1C2
Substituting the values:
1C′=13μF+16μF
Finding a common denominator (6):
1C′=26+16=36
Thus,
C′=63=2μF
Step 4: Calculate the Equivalent Capacitance of C3 and C4
Using the same formula for capacitors C3 and C4:
1C′′=1C3+1C4
Substituting the values:
1C′′=14μF+112μF
Finding a common denominator (12):
1C′′=312+112=412
Thus,
C′′=124=3μF
Step 5: Combine the Two Equivalent Capacitances
Now, C' and C'' are in parallel:
Ceq=C′+C′′
Substituting the values:
Ceq=2μF+3μF=5μF
Final Answer
The effective capacitance between points A and B is:
Ceq=5μF
We have four capacitors:
- C1 = 3μF
- C2 = 6μF
- C3 = 4μF
- C4 = 12μF
From the arrangement, we can see that:
- Capacitors C1 and C2 are in series.
- Capacitors C3 and C4 are also in series.
For capacitors in series, the formula for equivalent capacitance (C') is given by:
1C′=1C1+1C2
Substituting the values:
1C′=13μF+16μF
Finding a common denominator (6):
1C′=26+16=36
Thus,
C′=63=2μF
Using the same formula for capacitors C3 and C4:
1C′′=1C3+1C4
Substituting the values:
1C′′=14μF+112μF
Finding a common denominator (12):
1C′′=312+112=412
Thus,
C′′=124=3μF
Now, C' and C'' are in parallel:
Ceq=C′+C′′
Substituting the values:
Ceq=2μF+3μF=5μF
The effective capacitance between points A and B is:
Ceq=5μF
Similar Questions
Knowledge Check
What is the effective capacitance between A and B in the arrangement shown here?
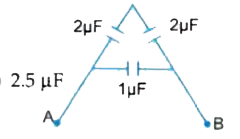 A1μFB2μFC1.5μFD2.5μF
A1μFB2μFC1.5μFD2.5μFFind the equivalent capacitance between A and B
 A5μFB4μFC3μFD2μF
A5μFB4μFC3μFD2μFThe effective capacitance between the points P and Q of the arrangement shown in the figure is
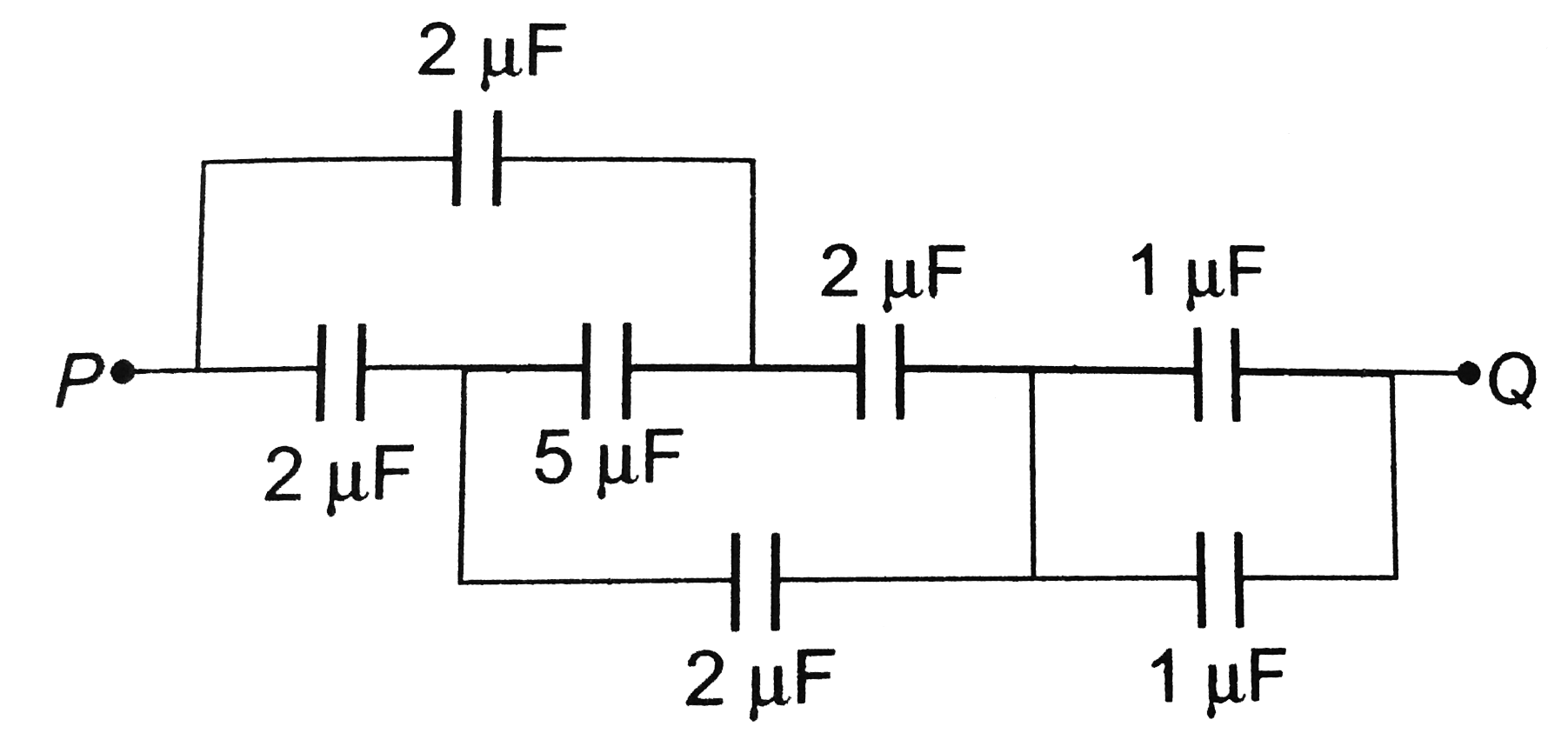 A12μFB1μFC2μFD1.33μF
A12μFB1μFC2μFD1.33μF