A capacitor with plate separation d is charged to V volts. The battery is disconnected and a dielectric slab of thickness d2 and dielectric constant '2' is inserted between the plates. The potential difference across its terminals becomes
V
2 V
4V3
3V4
The correct Answer is:D
To solve the problem step by step, let's break it down:
Step 1: Understanding the Initial Conditions
A capacitor is charged to a voltage V volts. When charged, the charge Q on the capacitor can be expressed as:
Q=C⋅V
where C is the capacitance of the capacitor.
Step 2: Disconnecting the Battery
Once the battery is disconnected, the charge Q remains constant. This means that the charge on the capacitor does not change when we insert the dielectric slab.
Step 3: Inserting the Dielectric Slab
A dielectric slab of thickness d2 and dielectric constant K=2 is inserted between the plates of the capacitor. The new configuration of the capacitor includes two regions:
1. The region with the dielectric slab (thickness d2).
2. The region without the dielectric (thickness d2).
Step 4: Calculating the New Capacitance
The capacitance of a capacitor can be calculated using the formula:
C=ε0Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
When the dielectric slab is inserted, the total capacitance C′ can be calculated as the sum of the capacitances of the two regions:
1. Capacitance of the region with the dielectric slab:
C1=Kε0Ad2=2ε0Ad2=4ε0Ad
2. Capacitance of the region without the dielectric:
C2=ε0Ad2=2ε0Ad
Step 5: Finding the Total Capacitance
Since the two capacitances are in series, the total capacitance C′ can be calculated using the formula for capacitors in series:
1C′=1C1+1C2
Substituting the values:
1C′=14ε0Ad+12ε0Ad
1C′=d4ε0A+d2ε0A=d4ε0A+2d4ε0A=3d4ε0A
Thus,
C′=4ε0A3d
Step 6: Calculating the New Potential Difference
The new potential difference V′ across the capacitor can be expressed as:
V′=QC′
Substituting C′:
V′=Q4ε0A3d=3dQ4ε0A
Since Q=C⋅V and C=ε0Ad, we can substitute Q:
V′=3d(ε0AdV)4ε0A=3V4
Conclusion
The new potential difference across the terminals of the capacitor after inserting the dielectric slab is:
V′=3V4
A capacitor is charged to a voltage V volts. When charged, the charge Q on the capacitor can be expressed as:
Q=C⋅V
where C is the capacitance of the capacitor.
Once the battery is disconnected, the charge Q remains constant. This means that the charge on the capacitor does not change when we insert the dielectric slab.
A dielectric slab of thickness d2 and dielectric constant K=2 is inserted between the plates of the capacitor. The new configuration of the capacitor includes two regions:
1. The region with the dielectric slab (thickness d2).
2. The region without the dielectric (thickness d2).
The capacitance of a capacitor can be calculated using the formula:
C=ε0Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
C1=Kε0Ad2=2ε0Ad2=4ε0Ad
C2=ε0Ad2=2ε0Ad
Since the two capacitances are in series, the total capacitance C′ can be calculated using the formula for capacitors in series:
1C′=1C1+1C2
Substituting the values:
1C′=14ε0Ad+12ε0Ad
1C′=d4ε0A+d2ε0A=d4ε0A+2d4ε0A=3d4ε0A
Thus,
C′=4ε0A3d
The new potential difference V′ across the capacitor can be expressed as:
V′=QC′
Substituting C′:
V′=Q4ε0A3d=3dQ4ε0A
Since Q=C⋅V and C=ε0Ad, we can substitute Q:
V′=3d(ε0AdV)4ε0A=3V4
The new potential difference across the terminals of the capacitor after inserting the dielectric slab is:
V′=3V4
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTEChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - B
Explore 38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTEChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - C
Explore 53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTEChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXERCISE
Explore 20 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
- GRAVITATION Book:AAKASH INSTITUTEChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 16 Videos
Similar Questions
A capacitor plates are charged by a battery with ‘V’ volts. After charging battery is disconnected and a dielectric slab with dielectric constant ‘K’ is inserted between its plates, the potential across the plates of a capacitor will become
View SolutionA parallel plate capacitor each with plate area A and separation ‘d’ is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now placed between the plates. What change if any, will take place in
(i) charge on the plates
(ii) electric field intensity between the plates,
(iii) capacitance of the capacitor
Justify your answer in each case
View Solution
Knowledge Check
A capacitor with plate separation d is charged to V volts. The battery is disconnected and a dielectric slab of thickness d2 and dielectric constant '2' is inserted between the plates. The potential difference across its terminals becomes
AVB2 VC4V3D3V4A capacitor plates are charged by a battery with ‘V’ volts. After charging battery is disconnected and a dielectric slab with dielectric constant ‘K’ is inserted between its plates, the potential across the plates of a capacitor will become
AZeroBV2CVkDKVSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
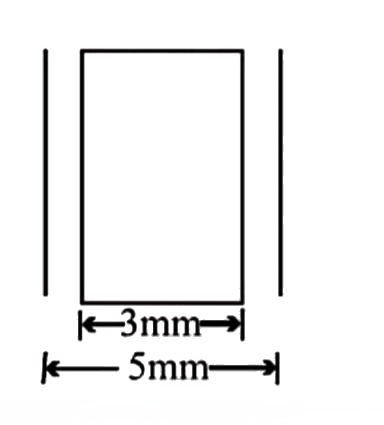 A18.5VB13.5VC11.5VD6.5V
A18.5VB13.5VC11.5VD6.5V
A parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
electric filed intensity between the plates ? Justify your answer .
View SolutionA parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
charge on plates ?
Justify your answer
View SolutionA parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
capacitance of the capacitor ? Justify your answer .
View SolutionA parallel plate capacitor is charged by a battery . After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates . How will potential difference between the plates ? Justify your answer
View SolutionFigure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dielectric constant K is placed in between the plates of the capacitor as shown.

The electric field in the dielectric slab is
View Solution