There exists a uniform electric field E =4 ×105Vm−3 directed along negative x-axis such that electric potential at origin is zero. A charge of - 200 μC is placed at origin and a charged of + 200 μ C is placed at a (3 m, 0) . The electrostatic potential energy of the system is
120 J
−120 J
−240 J
zero
The correct Answer is:A
To find the electrostatic potential energy of the system, we will consider the contributions from both the interaction between the two charges and the work done by the electric field on the charges.
1. Identify the Charges and Their Positions:
- Charge q1=−200μC=−200×10−6C is placed at the origin (0, 0).
- Charge q2=+200μC=+200×10−6C is placed at the point (3 m, 0).
2. Calculate the Distance Between the Charges:
- The distance r between the charges is 3m.
3. Use the Formula for Electrostatic Potential Energy:
- The formula for the potential energy U between two point charges is given by:
U=kq1q2r
where k=9×109Nm2/C2.
4. Substitute the Values into the Formula:
- Substitute q1, q2, and r into the equation:
U=9×109(−200×10−6)(200×10−6)3
5. Calculate the Product of Charges:
- Calculate q1q2:
q1q2=(−200×10−6)(200×10−6)=−40×10−12C2
6. Substitute Back to Find U:
- Now substitute back into the potential energy formula:
U=9×109−40×10−123
7. Calculate the Final Value of U:
- Simplifying gives:
U=9×109×(−403×10−12)=−120×10−3J
- Therefore, the electrostatic potential energy U is:
U=−0.12J
Final Answer:
The electrostatic potential energy of the system is −0.12J.
- Charge q1=−200μC=−200×10−6C is placed at the origin (0, 0).
- Charge q2=+200μC=+200×10−6C is placed at the point (3 m, 0).
- The distance r between the charges is 3m.
- The formula for the potential energy U between two point charges is given by:
U=kq1q2r
where k=9×109Nm2/C2.
- Substitute q1, q2, and r into the equation:
U=9×109(−200×10−6)(200×10−6)3
- Calculate q1q2:
q1q2=(−200×10−6)(200×10−6)=−40×10−12C2
- Now substitute back into the potential energy formula:
U=9×109−40×10−123
- Simplifying gives:
U=9×109×(−403×10−12)=−120×10−3J
- Therefore, the electrostatic potential energy U is:
U=−0.12J
The electrostatic potential energy of the system is −0.12J.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - C
53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
47 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
Similar Questions
Knowledge Check
There exists a uniform electric field E=4×105Vm−1 directed along negative x-axis such that electric potential at origin is zero. A charge of −200μC is palced at origin, and a charge of +200μC is placed at (3m,0). The electrostatic potential energy of the system is
A120JB−120JC−240JDzeroA charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
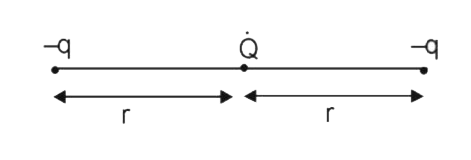
A−(4.32ˆi+5.76ˆj)×102N/CB−(4.32ˆi−5.76ˆj)×102N/CC−(5.76ˆi+4.32ˆj)×102N/CD(4.32ˆi+5.76ˆj)×102N/CThree charges are placed along x-axis at x = - a x = 0 and x = a as shown in the figure. The potential energy of the system is
 A−(14πε0)q2aB−(14πε0)3q22aC+(14πε0)q2aD+(14πε0)3q22a
A−(14πε0)q2aB−(14πε0)3q22aC+(14πε0)q2aD+(14πε0)3q22a
A point charge of 0.01 μC is placed at the origin. Calculate the electric field at another point charge of 0.05 μC placed at (0 m, 5 m).
View SolutionA point charge of 10mC is placed at origin.The value of electric potential at point (3,4)m is.........
View SolutionLet there be a uniform electric field "E" existing along the positive X-direction.Assume electric potential to be zero at the origin.Potential at the point x=x0 is
View SolutionA positive charge of 20μC is placed 2 m away from a negative charge of 20μC. Determine the electric field at a point 2 m away from each charges.
View SolutionA positive charge of 20μC is placed 2 m away from a negative charge of 20μC. Determine the electric field at a point 2 m away from each charges.
View Solution