There are two indetical capacitor , the first one is uncharged and filled with dielectric of constant K while the other one is charged to potential v having air between its plates, if two capacitors are joined end to end, the common potential will be
VK−1
KVK+1
KVK−1
VK+1
The correct Answer is:D
To solve the problem step by step, we will follow these steps:
Step 1: Understand the Capacitors
We have two identical capacitors:
- Capacitor 1 (C1) is uncharged and filled with a dielectric of constant K.
- Capacitor 2 (C2) is charged to a potential V and has air between its plates.
Step 2: Determine the Capacitance Values
- The capacitance of Capacitor 1 (C1) with dielectric is given by:
C1=K⋅C
where C is the capacitance of the capacitor without the dielectric.
- The capacitance of Capacitor 2 (C2) with air is:
C2=C
Step 3: Identify Initial Conditions
- The initial voltage across Capacitor 1 (V1) is:
V1=0(since it is uncharged)
- The initial voltage across Capacitor 2 (V2) is:
V2=V(since it is charged to potential V)
Step 4: Apply the Formula for Common Potential
When the two capacitors are connected end to end, the common potential (V_common) can be calculated using the formula:
Vcommon=C1V1+C2V2C1+C2
Step 5: Substitute the Values
Substituting the values we have:
Vcommon=(K⋅C)(0)+(C)(V)(K⋅C)+C
This simplifies to:
Vcommon=0+CVKC+C
Vcommon=CVC(K+1)
Step 6: Simplify the Expression
We can cancel C from the numerator and denominator:
Vcommon=VK+1
Step 7: Conclusion
Thus, the common potential when the two capacitors are connected end to end is:
VK+1
---
We have two identical capacitors:
- Capacitor 1 (C1) is uncharged and filled with a dielectric of constant K.
- Capacitor 2 (C2) is charged to a potential V and has air between its plates.
- The capacitance of Capacitor 1 (C1) with dielectric is given by:
C1=K⋅C
where C is the capacitance of the capacitor without the dielectric.
- The capacitance of Capacitor 2 (C2) with air is:
C2=C
- The initial voltage across Capacitor 1 (V1) is:
V1=0(since it is uncharged)
- The initial voltage across Capacitor 2 (V2) is:
V2=V(since it is charged to potential V)
When the two capacitors are connected end to end, the common potential (V_common) can be calculated using the formula:
Vcommon=C1V1+C2V2C1+C2
Substituting the values we have:
Vcommon=(K⋅C)(0)+(C)(V)(K⋅C)+C
Vcommon=0+CVKC+C
Vcommon=CVC(K+1)
We can cancel C from the numerator and denominator:
Vcommon=VK+1
Thus, the common potential when the two capacitors are connected end to end is:
VK+1
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - C
53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
47 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
Similar Questions
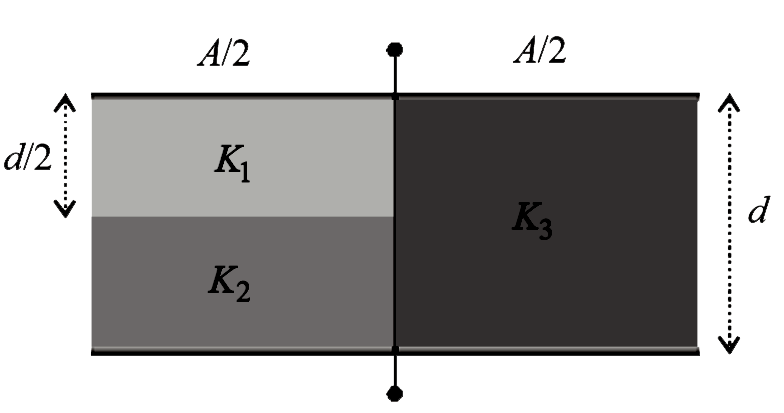
Two dielectric slabs of constant K1 and K2 have been filled in between the plates of a capacitor as shown below. What will be the capacitance of the capacitor
View SolutionIf a capacitor connected to a battery is fully charged, then a dielectric (k) is inserted between plates then increase in the potential energy is
View Solution
Knowledge Check
In a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
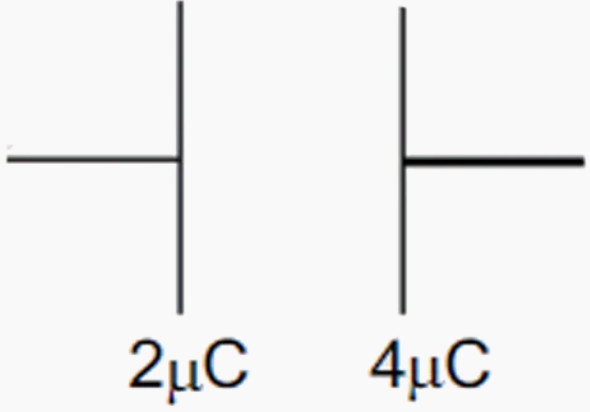 A2 voltB1 voltC4 voltD3 volt
A2 voltB1 voltC4 voltD3 voltAn unchanged parallel plate capacitor filled wit a dielectric constant K is connect to an air filled identical parallel capacitor charged to potential V1. It the common potential is V2, the value of K is
AV1−V2V1BV1V1−V2CV2V1−V2DV1−V2V2A parallel-plate capacitor is filled with a dielectric upto one-half of the distance between the plates. The manner in which, the potential between the plates varies is illustrated in the figure
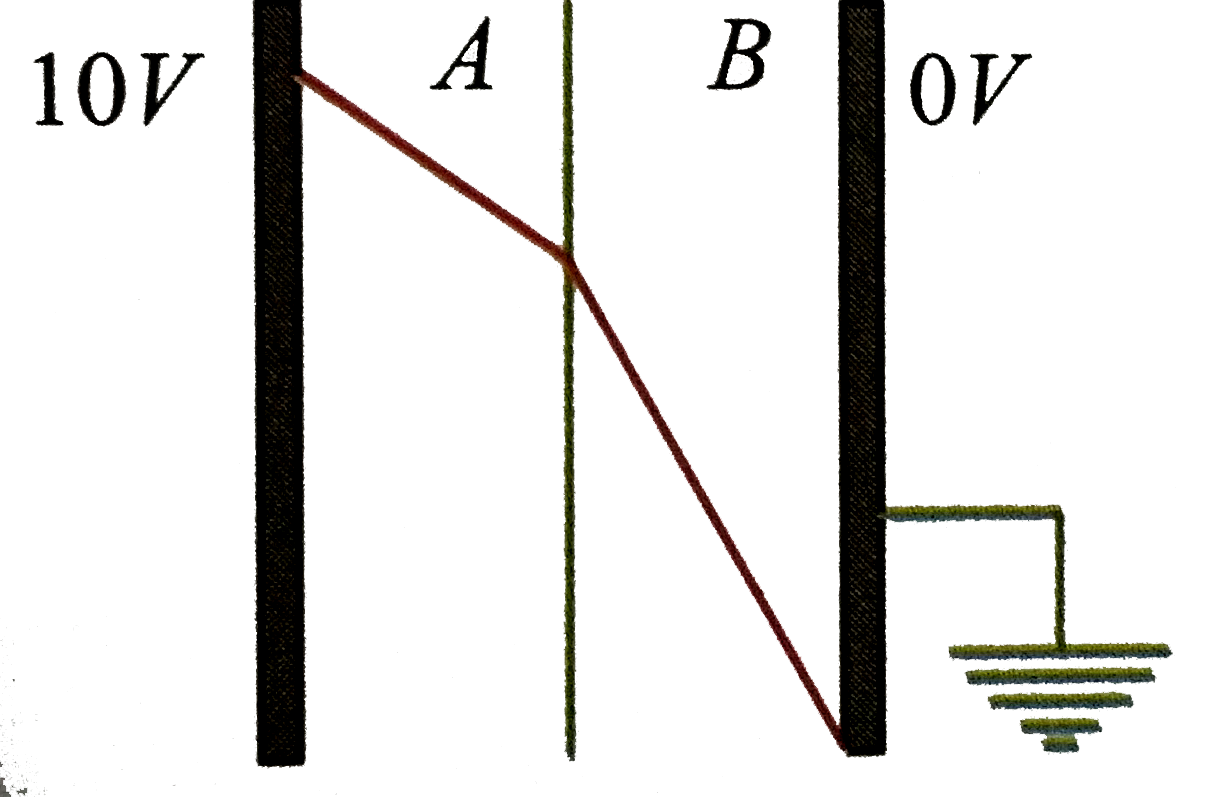 .AThe electroc field strength is greater in part ABThe electric field strength is greater in part BCDielectric slab fills the space of part ADDielectric slab fills the space of part B
.AThe electroc field strength is greater in part ABThe electric field strength is greater in part BCDielectric slab fills the space of part ADDielectric slab fills the space of part B
A parallel plate capacitor of capacitance C has been charged, so that the potential difference between its plates is V. Now, the plates of this capacitor are connected to another uncharged capacitor of capacitance 2C. Find the common potential acquired by the system and loss of energy.
View SolutionA parallel - plate capacitor of plate area Aand plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View Solutionn capacitors identical to each other joined in parallel are charged to a common potential V. The battery is disconnected. Now the capacitors are joined in series. For the new combination:
View SolutionAn uncharge parallel plate capacitor having a dielectric of dielectric constant K is connected to a similar air coare parallel plate capacitor charged to a potential V0. The two share the charge, and the common potential becomes V. The dielectric constant K is
View SolutionA parallel plate capacitor with a dielectric slab with dielectric constant k=3 filling the space between the plates is charged to potential V and isolated. Then the dielectric slab is drawn out and another dielectric slab of equal thickness but dielectric constant k'=2 is introduced between the plates. The ratio of the energy stored in the capacitor later to that initially is:
View Solution
