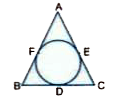
Incircle of $Δ A B C$ touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
The length of side EF is

$r sin . \frac{A}{2}$

$2 r sin . \frac{A}{2}$

$r cos . \frac{A}{2}$

$2 r cos . \frac{A}{2}$

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Incircle of $Δ A B C$ touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
Area of $Δ D E F$ is
A $2 r^{2} sin (2 A) sin (2 B) sin (2 C)$
B $2 r^{2} cos . \frac{A}{2} cos . \frac{B}{2} cos . \frac{C}{2}$
C $2 r^{2} sin (A - B) sin (B - C) sin (C - A)$
Dnone of these
Incircle of $Δ A B C$ touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
$∠ D E F$ is equal to
A $\frac{π - B}{2}$
B $π - 2 B$
C $A - C$
Dnone of these
The in circle of $Δ A B C$ touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
A $\frac{1}{2}$ (Perimeter of $Δ$ ABC)
B $\frac{1}{3}$ (Perimeter of $Δ$ ABC)
C $\frac{1}{4}$ (Perimeter of $Δ$ ABC)
DPerimeter of $Δ$ ABC