In ΔABC,P,Q,R are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. ΔPQR is constructed

If ∠BAC=120∘, then measusred of ∠RPQ will be
60∘
90∘
120∘
150∘
The correct Answer is:B
Since C is the excentre of ΔAB, we have

∠APQ=∠QPC
Also, R is the excentre of ΔAPC
so, ∠APR=∠RPS
so, ∠RPQ=90∘
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Matrix)
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Numerical)
22 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Multiple)
24 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
In △ABC,P,Q,R are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. △PQR is constructed
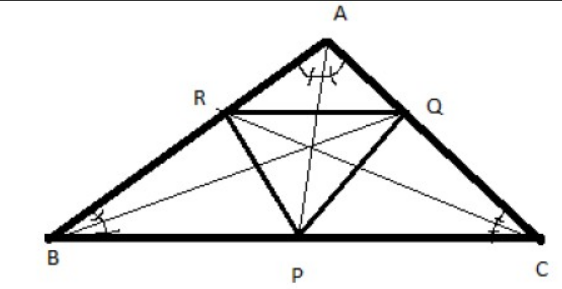
If AB=7 units, BC = 8 units, AC = 5 units, then the side PQ will be
View SolutionIf in a ΔABC, the altitudes from the vertices A, B, C on opposite sides are in H.P, then sin A, sin B, sin C are in
View Solution
Knowledge Check
In ΔABC,P,Q,R are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. ΔPQR is constructed

If AB=7 units, BC = 8 units, AC = 5 units, then the side PQ will beA√283 unitsB√883 unitsC√783 unitsD√843 unitsIf in ΔABC,AB=AC (see figure), BP and CQ be the altitudes from the vertices to their opposite sides, then
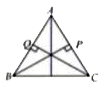 ABP=CQBAP=AQC∠ABC=∠ACBDAll of these
ABP=CQBAP=AQC∠ABC=∠ACBDAll of these
If in a triangle ABCp.q.r are the altitudes from the vertices A,B,C to the opposite sides, then which of the following does not hold good ?
View SolutionIf ΔABC is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionIf ΔABC is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionIn ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
CB:BA=CP:PA
View SolutionIn ΔABC exterior angle bisectors of ∠Band∠C meets at point P if ∠BAC=80∘ then find ∠BPC.
View SolutionIn ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
AB×BC=BP×CA
View Solution
