The Bernoulli's equation is given by P+12ρv2+hρg=k. Where P= pressure, ρ= density, v= speed, h=height of the liquid column, g= acceleration due to gravity and k is constant. The dimensional formula for k is same as that for:
Velocity gradient
Pressure gradient
Modulus of elasticity
Thrust
The correct Answer is:C
k is dimensionally equal to P
k=[M1L−1T−2]
Modulus of elasticity = StressStrain=F/AΔll=[ML−1T−2]
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-II AIIMS 20162videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION9videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)51videos
SEMICONDUCTORS
Similar Questions
Test if the following equation is dimensionally correct: h=(sScosθrpg) where h= height, S= surface tension, p= density, r=radius, and g= acceleration due to gravity.
View SolutionThe pressure at a depth h in a liquid of density d is given by pressure = __ , where g is the acceleration due to gravity.
View Solution
Knowledge Check
- Question 1 - Select One
According to Bernoulli's theorem pd+v22+gh = constant is (P is pressure, d is density, h is height, v is velocity and g is acceleration due to gravity)
A[M0L0T0]B[M0LT0]C[M0L2T−2]D[M0L2T−4] - Question 2 - Select One
Given as : h=2Scosθrρg where S is the surface tension of liquid, r is the radius of capillary tube. ρ is the density and g is acceleration due to gravity then dimensional formula for S is:
A[ML0T−2]B[M0LT−2]C[ML2T−2]D[M0L0T−3] - Question 3 - Select One
The height of liquid column in capillary tube is h the radius of capillary tube is r.ρ is the density of liquid , g is acceleration due to gravity and θ is angle of contact . The surface tension of the liquid is ,
At=rhρg2cosθBT=2cosθhρgrCT=2cosθrρhgDall of these
Check by the method of dimensions, whether the folllowing relation are dimensionally correct or not. (i) υ=√P/ρ, where υ is velocity. P is prerssure and ρ is density. (ii) v=2π√Ig, where I is length, g is acceleration due to gravity and v is frequency.
View SolutionA formula is given as P=ba√1+k.θ.t3m.a
where P = pressure, k = Boltzmann's constant,
θ= temperature, t= time, 'a' and 'b' are constants.
Dimensional formula of 'b' is same asView SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
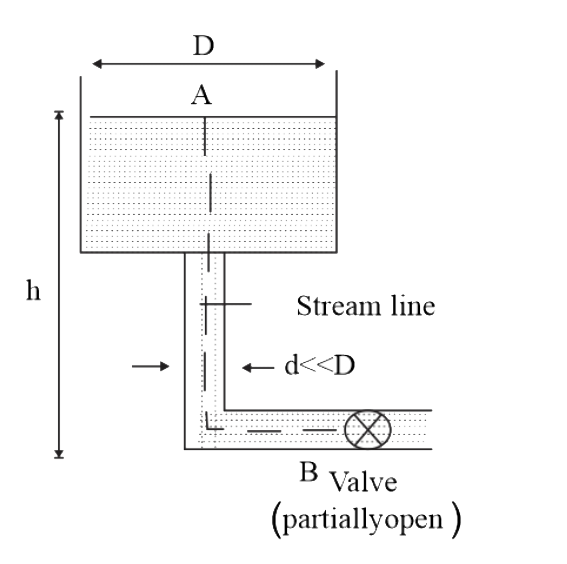 View Solution
View SolutionA liquid drop placed on a horizontal plane has a near spherical shape (slightly flattened due to gravity). Let R be the radius of its largest horizontal section. A small disturbance causes the drop to vibrate with frequency v about its equilibrium shape. By dimensional analysis the ratio v√σ/ρR3 can be (Here σ is surface tension, ρ is density, g is acceleration due to gravity, and k is arbitrary dimensionless constant)–
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View Solution

