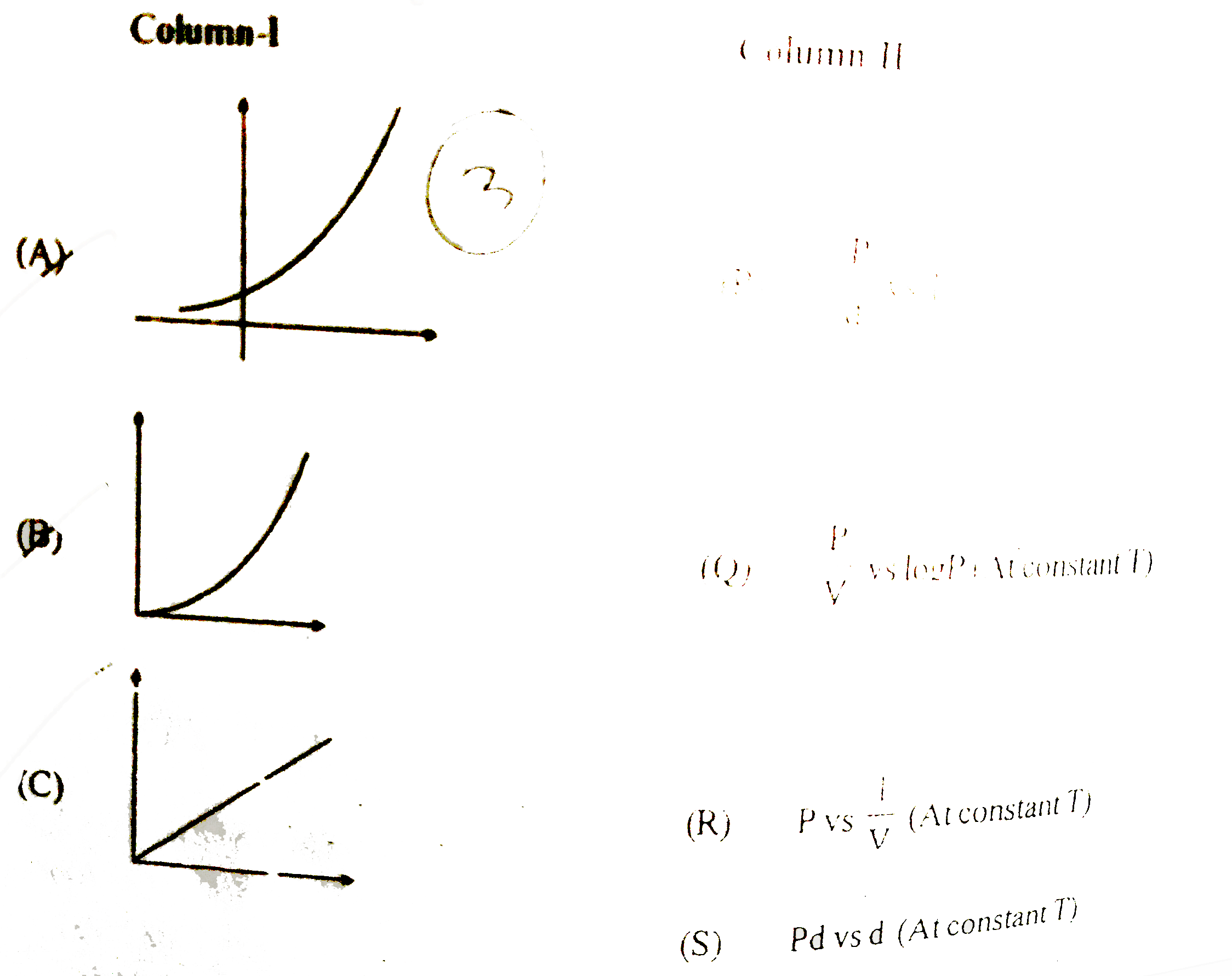At constant pressure , the volume of fixed mass of an ideal gas is directly proportional to
Absolute temperature
Degree contigrade
Degree Fahrenheit
None
The correct Answer is:A
To solve the question, we need to understand the relationship between the volume of an ideal gas and its temperature at constant pressure. This relationship is described by Charles's Law.
1. Understand the Ideal Gas Law: The ideal gas law is given by the equation:
PV=nRT
where P is the pressure, V is the volume, n is the number of moles, R is the gas constant, and T is the temperature.
2. Identify the Conditions: The question states that the pressure is constant and we have a fixed mass of gas. This means that P and n are constant.
3. Rearranging the Ideal Gas Law: Since P and n are constant, we can rearrange the ideal gas law to focus on volume and temperature:
V=nRTP
Since n, R, and P are constants, we can see that volume V is directly proportional to temperature T:
V∝T
4. Temperature in Kelvin: It is important to note that temperature T must be measured in Kelvin for this relationship to hold true. The Kelvin scale is the absolute temperature scale, where 0 Kelvin is absolute zero.
5. Conclusion: Therefore, at constant pressure, the volume of a fixed mass of an ideal gas is directly proportional to the absolute temperature (in Kelvin).
Final Answer:
The volume of a fixed mass of an ideal gas at constant pressure is directly proportional to absolute temperature.
PV=nRT
where P is the pressure, V is the volume, n is the number of moles, R is the gas constant, and T is the temperature.
V=nRTP
Since n, R, and P are constants, we can see that volume V is directly proportional to temperature T:
V∝T
The volume of a fixed mass of an ideal gas at constant pressure is directly proportional to absolute temperature.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - STATES OF MATTEREXERCISE - EXERCISE - 242videos
STATES OF MATTER
- BOOK - NARAYNACHAPTER - STATES OF MATTEREXERCISE - EXERCISE - 332videos
STATES OF MATTER
- BOOK - NARAYNACHAPTER - STATES OF MATTEREXERCISE - CUQ35videos
STATES OF MATTER
- BOOK - NARAYNACHAPTER - SOME BASIC PRINCIPLES AND TECHNIQUESEXERCISE - EXERCISE -IV (QUALITATIVE AND QUANTITATIVE ANALYSIS OF ORGANIC OF COMPOUNDS)8videos
SOME BASIC PRINCIPLES AND TECHNIQUES
- BOOK - NARAYNACHAPTER - STRUCTURE OF ATOMEXERCISE - EXERCISE - IV EXEMPLAR PROBLEMS24videos
STRUCTURE OF ATOM
Similar Questions
Knowledge Check
- Question 1 - Select One
The pressure of an ideal gas is directly proportional to
Atotal kinetic energyBtranslational kinetic energyCrotational kinetic energyDvibrational kinetic energy - Question 2 - Select One
Pressure is directly proportional to
AForceBThrustCAreaDVelocity - Question 3 - Select One
Pressure is directly proportional to
AForceBThrustCAreaDVelocity
At constant volume the pressure of a given mass of a gas is directly proportional to its absolute temperature is known
View SolutionThe volume of a nucleus is directly proportional to
View SolutionAt constant pressure , the volume of a fixed mass of a gas varies as a function of temperarture as shown in the graph
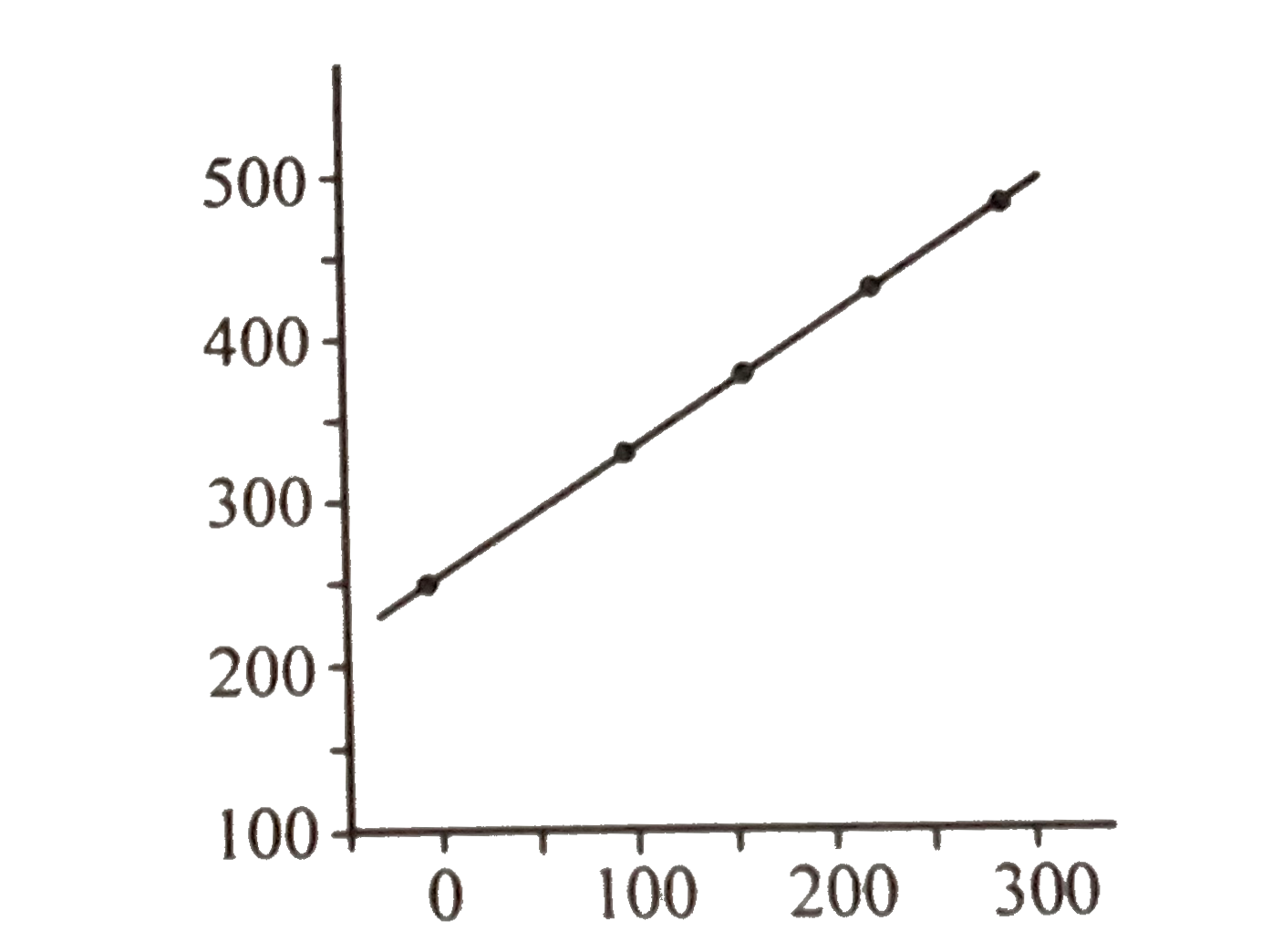
the volume of the gas 300∘C is larger than at 0∘C by a factor ofView SolutionAssertion: At constant temperature, if pressure on the gas is doubled, density is also doubled.
Reason: At constant temperature, molecular mass of a gas is directly proportional to the density and inversely proportional to the pressureView SolutionWhich law states that the volume of an ideal gas at constant pressure is directly proportional to the absolute temperature?
View Solution