If the activation energy of both the forward and the backward reactions are equal, then change in internal energy is
zero
+Ve
−Ve
cannot be predicted
The correct Answer is:A
To solve the problem, we need to analyze the relationship between activation energy, enthalpy change, and internal energy change in a chemical reaction. Here’s a step-by-step breakdown:
Step 1: Understand Activation Energy
Activation energy (Ea) is the minimum energy required for a chemical reaction to occur. In this case, we have two activation energies: one for the forward reaction (Ea forward) and one for the backward reaction (Ea backward).
Step 2: Given Condition
The problem states that the activation energies for both the forward and backward reactions are equal:
Ea (forward)=Ea (backward)
Step 3: Energy Profile Diagram
To visualize this, we can draw an energy profile diagram. The x-axis represents the progress of the reaction, while the y-axis represents energy.
- The reactants start at a certain energy level.
- The products will also end at the same energy level since the activation energies are equal.
Step 4: Change in Enthalpy (ΔH)
The change in enthalpy (ΔH) for a reaction is calculated as:
ΔH=Ea (forward)−Ea (backward)
Since both activation energies are equal, we can substitute:
ΔH=Ea−Ea=0
Step 5: Change in Internal Energy (ΔE)
The change in internal energy (ΔE) is related to the change in enthalpy (ΔH) by the equation:
ΔE=ΔH+PΔV
In this case, we are not considering any volume change (assuming constant pressure and volume), so:
ΔE=ΔH
Since we found that ΔH = 0, it follows that:
ΔE=0
Conclusion
Therefore, if the activation energy of both the forward and backward reactions are equal, the change in internal energy (ΔE) is:
ΔE=0
Final Answer
The change in internal energy is 0.
---
Activation energy (Ea) is the minimum energy required for a chemical reaction to occur. In this case, we have two activation energies: one for the forward reaction (Ea forward) and one for the backward reaction (Ea backward).
The problem states that the activation energies for both the forward and backward reactions are equal:
Ea (forward)=Ea (backward)
To visualize this, we can draw an energy profile diagram. The x-axis represents the progress of the reaction, while the y-axis represents energy.
- The reactants start at a certain energy level.
- The products will also end at the same energy level since the activation energies are equal.
The change in enthalpy (ΔH) for a reaction is calculated as:
ΔH=Ea (forward)−Ea (backward)
ΔH=Ea−Ea=0
The change in internal energy (ΔE) is related to the change in enthalpy (ΔH) by the equation:
ΔE=ΔH+PΔV
In this case, we are not considering any volume change (assuming constant pressure and volume), so:
ΔE=ΔH
Since we found that ΔH = 0, it follows that:
ΔE=0
Therefore, if the activation energy of both the forward and backward reactions are equal, the change in internal energy (ΔE) is:
ΔE=0
The change in internal energy is 0.
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (RATE OF REACTION & FACTORS)
14 Videos
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (ORDER OF REACTION)
14 Videos
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - CHECK YOUR GRASP
14 Videos
- CARBOXYLIC ACIDBOOK - NARAYNACHAPTER - CARBOXYLIC ACIDEXERCISE - All Questions
288 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - NARAYNACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ASSERTION & REASON TYPE QUESTIONS
10 Videos
Similar Questions
The rate of a gaseous reaction is given by the expression k [A] [B]. If the volume of the reaction vessel is suddenly reduced to 1/4th of the initial volume, the reaction rate relating to original rate will be
View Solutionfor a reaction 2A+3B→Products, the rate law expression is given by rate = K(A)1(B)2 . The order of the reaction with respect to A,B and over all order of reaction ar
View SolutionWhat is the instantaneous rate of a reaction.
View SolutionProvide IUPAC name of the compound given below.
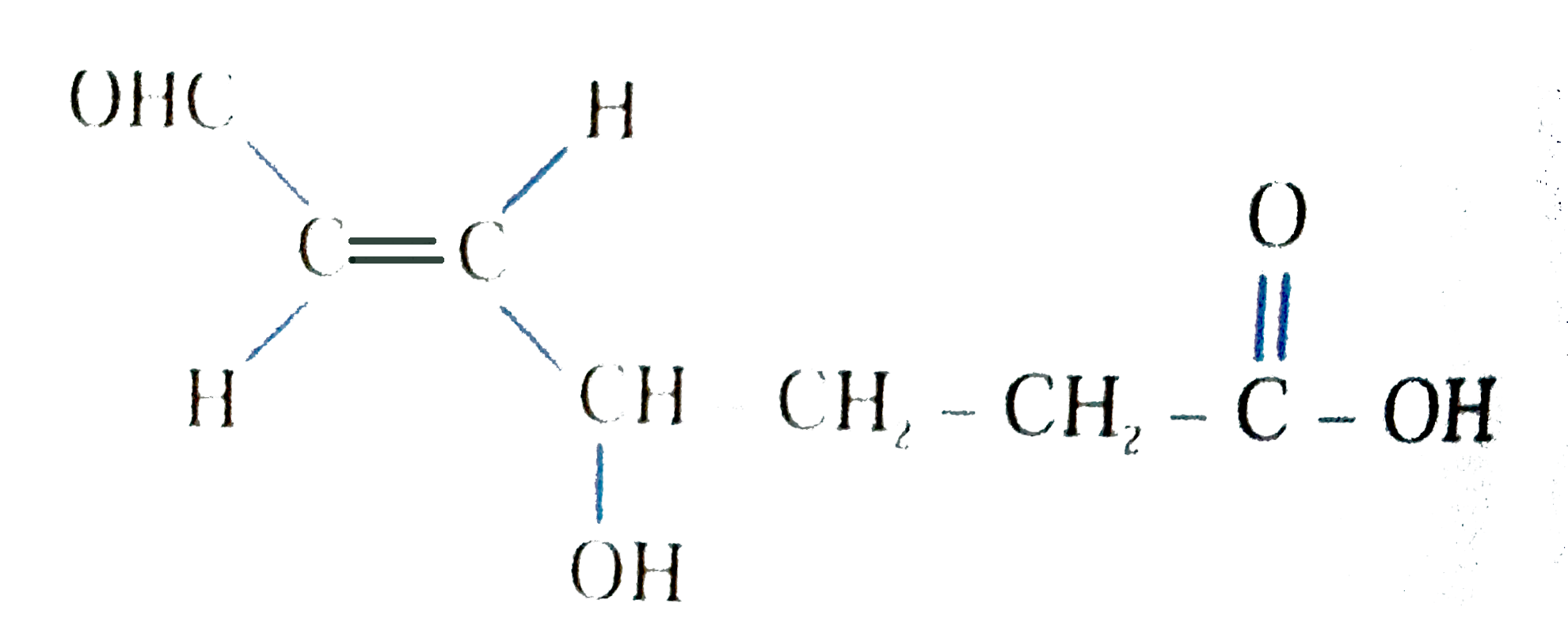
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View SolutionEnergy of activation of forward and backward reaction are equal in case (numerical calues) where
View SolutionFor the reaction, for which the activation energies for forward and backward reactions are same, then:
View SolutionWhen the activation energies of the forward and backward reactions are equal, then :
View SolutionIn the presence of catalyst, activation energy for forward reaction……………………, that for backward reaction………………..and the value of enthalpy change…………………….. .
View SolutionA+BrarrC-50kJ, in this reaction, the energy of activation of backward reaction is 18 kJ . Calculate the activation energy of forward reaction.
View SolutionEnergy of activation of forward reaction for an endothermic process is 50kJ. If enthalpy change for forward reaction is 20kJ then enthalpy change for backward reaction will be-
View SolutionA : For exothermic reaction, DeltaH=E_a (forward) -E_a (backward) R : The value of activation energy for forward direction is less than activation energy for backward reaction.
View SolutionThe activation energies for forward and backward reactions are E_f and E_b respectively. If the reaction is exothermic then which is true regarding relation of activation energies?
View SolutionIn a reversible reaction, the enthalpy change and the activation energy in the forward direction are respectively -xkJmol and y kJ mol ^(-1) . Therefore , the energy of activation in the backward direction is ........
View Solution(A) The addition of catalyst lowers the activation barrier, yet there is no change in the enthalpy of reaction.
(R ) Enthalpy change is equal to the difference in the activation energy for the forward and the backward reactions.
View Solution
