The rate constant (K1) of one reaction is found to be double that of the rate constant of (K2) another reaction. Then the relationship - ' between the corresponding activation energies of two reactions (E1andE2) can be represented.
E1>E2
E1<E2
E1=E2
E1=4E2
The correct Answer is:B
To find the relationship between the activation energies E1 and E2 of two reactions with rate constants K1 and K2, where K1=2K2, we can use the Arrhenius equation, which relates the rate constant to the activation energy.
1. Write the Arrhenius Equation for Both Reactions:
The Arrhenius equation is given by:
K=Ae−ERT
For the first reaction:
K1=A1e−E1RT
For the second reaction:
K2=A2e−E2RT
2. Substitute the Given Relationship:
According to the problem, K1=2K2. Thus, we can write:
A1e−E1RT=2(A2e−E2RT)
3. Rearranging the Equation:
We can rearrange this equation to isolate the exponential terms:
A1A2=2e−E1−E2RT
4. Taking Natural Logarithm:
Taking the natural logarithm of both sides gives:
ln(A1A2)=ln(2)−E1−E2RT
5. Rearranging for Activation Energies:
Rearranging this equation, we can express the difference in activation energies:
E1−E2RT=ln(2)−ln(A1A2)
This implies:
E1−E2=RT(ln(2)−ln(A1A2))
6. Conclusion on Activation Energies:
Since RTln(2) is a positive term, we can conclude that:
E2>E1
This means the activation energy for the second reaction is greater than that of the first reaction.
Final Relationship:
E2>E1
The Arrhenius equation is given by:
K=Ae−ERT
For the first reaction:
K1=A1e−E1RT
For the second reaction:
K2=A2e−E2RT
According to the problem, K1=2K2. Thus, we can write:
A1e−E1RT=2(A2e−E2RT)
We can rearrange this equation to isolate the exponential terms:
A1A2=2e−E1−E2RT
Taking the natural logarithm of both sides gives:
ln(A1A2)=ln(2)−E1−E2RT
Rearranging this equation, we can express the difference in activation energies:
E1−E2RT=ln(2)−ln(A1A2)
This implies:
E1−E2=RT(ln(2)−ln(A1A2))
Since RTln(2) is a positive term, we can conclude that:
E2>E1
This means the activation energy for the second reaction is greater than that of the first reaction.
E2>E1
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (RATE OF REACTION & FACTORS)14videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (ORDER OF REACTION)14videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - CHECK YOUR GRASP14videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CARBOXYLIC ACIDEXERCISE - All Questions288videos
CARBOXYLIC ACID
- BOOK - NARAYNACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ASSERTION & REASON TYPE QUESTIONS10videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
The rate of a gaseous reaction is given by the expression k [A] [B]. If the volume of the reaction vessel is suddenly reduced to 1/4th of the initial volume, the reaction rate relating to original rate will be
03:57View Solutionfor a reaction 2A+3B→Products, the rate law expression is given by rate = K(A)1(B)2 . The order of the reaction with respect to A,B and over all order of reaction ar
04:03View SolutionWhat is the instantaneous rate of a reaction.
03:15View SolutionProvide IUPAC name of the compound given below.
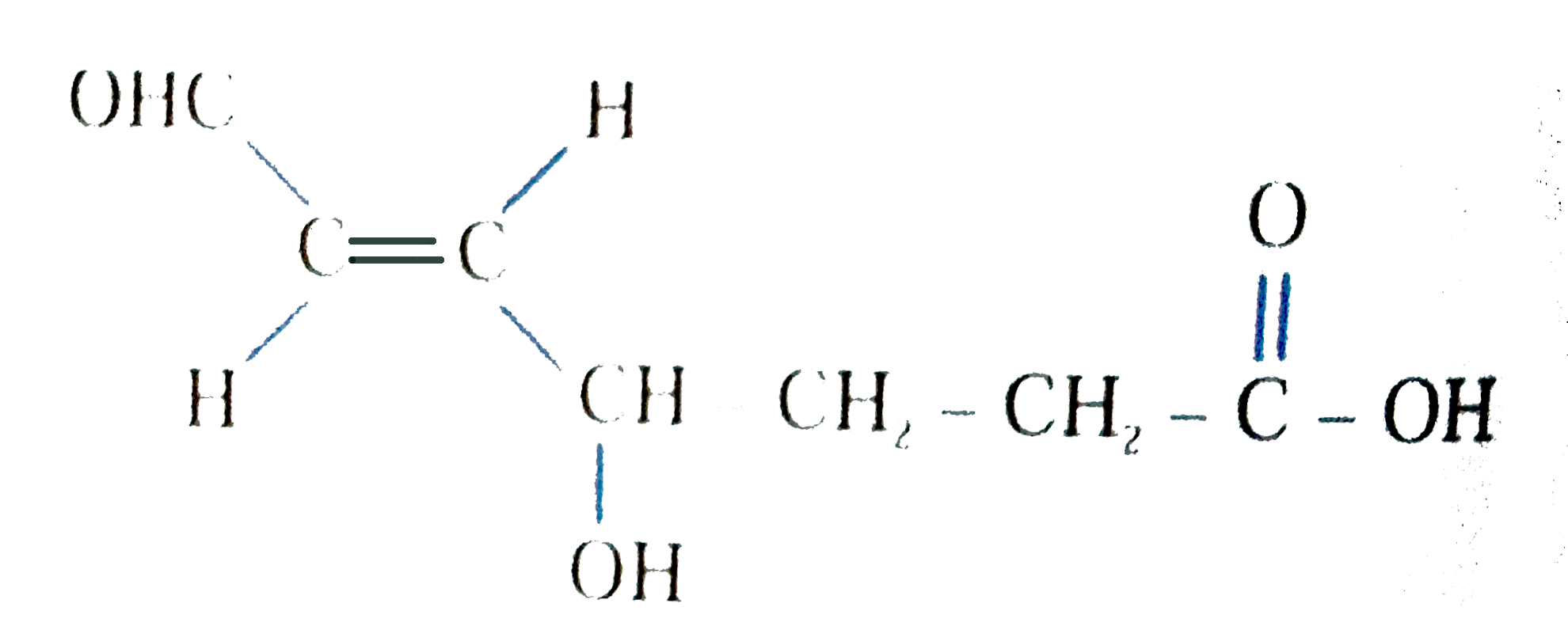 03:55View Solution
03:55View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.01:28View SolutionA reaction takes place in theee steps: the rate constant are k_(1), k_(2), and k_(3) . The overall rate constant k=(k_(1)k_(3))/(k_(2)) . If E_(1), E_(2) , and E_(3) (energy of activation) are 60, 30 and 10kJ , respectively, the overall energy of activation is
04:46View SolutionThe rate constant K1 of a reaction is found to be double that of rate constant K2 of another reaction. The relationship between corresponding activation energies of the two reaction at same temperature (E1andE2) can be represented as:
03:15View SolutionThe rate constant (K') of one reaction is double of the rate constant (K") of another reaction. Then the relationship between the corresponding activation energies of the two reactions (E_(a)^(') "and" E_(a)^('')) will be
View SolutionThe activation energies of two reactions are E_(1) & E_(2) with E_(1)gtE_(2) . If temperature of reacting system is increased from T_(1) (rate constant are k_(1) and k_(2) ) to T_(2) (rate constant are k_(1)^(1) and k_(2)^(1) ) predict which of the following alternative is incorrect.
05:48View SolutionA reaction takes place in three steps. The rate constant are k1,k2 and k3. The overall rate constant k=k1k3k2. If E1,E2 and E3 (energy of activation) are 60, 30 and 10 kJ, respectively, the overall energy. Of activation is
02:00View SolutionThe rate constant (k1) of one of the reactions is found to be double than that of the rate constant (k2) of another reaction. The relationship between the corresponding activation energies of the two reactions Ea1<Ea2
02:00View SolutionThe rate constant (K') of one reaction is double of the rate constant (K") of another reaction. Then the relationship between the corresponding activation energies of the two reactions (E′aandE''a) will be
04:53View SolutionThe rate constant (k') of one of the reaction is found to be double that of the rate constant (k") of another reaction. Then the relationship between the corresponding activation energies of the two reactions can be represented as
02:37View Solutionदो विभिन्न तापमानों (T1 तथा T2) पर एक अभिक्रिया की सक्रियण ऊर्जा (Ea) तथा दर नियतांक (k1तथा k2) इस प्रकार सम्बन्धित हैं-
01:42View SolutionThe rate constant K1 of a reaction is found to be double that of rate constant K2 of another reaction. The relationship between corresponding activation energies of the two reactions E1 and E2 can be represented as
01:30View Solution

