If one star equals four circles and three circles equal four diamonds, then what is the ratio of star to diamond? 1:3 b. 3:4 c. 3:16 d. 16:3
To solve the problem, we need to find the ratio of stars (S) to diamonds (D) based on the given relationships between stars, circles, and diamonds.
1. Understand the relationships given:
- We know that 1 star (S) equals 4 circles (C).
- We also know that 3 circles (C) equal 4 diamonds (D).
2. Express circles in terms of diamonds:
- From the second relationship, we can express circles in terms of diamonds:
3C=4D⟹C=43D
3. Substitute circles in the first relationship:
- Now we substitute the value of C in the first relationship:
1S=4C⟹1S=4(43D)
- Simplifying this gives:
1S=163D
4. Find the ratio of stars to diamonds:
- To find the ratio of stars (S) to diamonds (D), we can rearrange the equation:
S=163D⟹SD=163
5. Express the ratio:
- Therefore, the ratio of stars to diamonds is:
S:D=16:3
Final Answer:
The ratio of stars to diamonds is 16:3, which corresponds to option d.
---
- We know that 1 star (S) equals 4 circles (C).
- We also know that 3 circles (C) equal 4 diamonds (D).
- From the second relationship, we can express circles in terms of diamonds:
3C=4D⟹C=43D
- Now we substitute the value of C in the first relationship:
1S=4C⟹1S=4(43D)
- Simplifying this gives:
1S=163D
- To find the ratio of stars (S) to diamonds (D), we can rearrange the equation:
S=163D⟹SD=163
- Therefore, the ratio of stars to diamonds is:
S:D=16:3
The ratio of stars to diamonds is 16:3, which corresponds to option d.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the perimeter of circle A is equal to perimeter of semi circle B, what is the ratio of their areas ?
A(π+2)2:2π2B2π2:(π+2)2C(π+2)2:4π2D4π2:(π+2)2If the four equal circles of radius 3 cm touch each other externally, then the area of the region bounded by the four circles is
A4(9−π) sq. cmB9(4−π) sq. cm.C5(6−π) sq. cm.D6(5−π) sq. cm163/4 is equal to :
A4√2B8C2√2D16
From a circular sheet of paper with radius 20 cm, four circles of radius 5 cm each are cut out. What is the ratio of the uncut to the cut portion? (a) 1 : 3 (b) 3 : 1 (c) 4 : 1 (d) 4 : 3
View SolutionFive mangoes and four oranges cost as much as three mangoes and seven oranges. What is the ratio of the cost of one mango to the cost of one orange? 4:3 b. 1:3 c. 3:2 d. 5:2
View SolutionThe volumes of two spheres are in the ratio of 64 : 27. The ratio of their surface areas is (a) 1 : 2 (b) 2 : 3 (c) 9 : 16 (d) 16 : 9
View SolutionABCD is a square, in which a circle is inscribed touching all the sides of square. In the four corners of square 4 smaller circles of equal radii are drawn, containing maximum possible area.
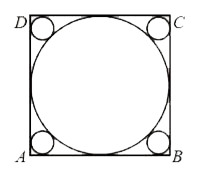
What is the ratio of the area of larger circle to that of sum of the areas of four smaller circles?
(a) 1:(68−48√2)
(b)1:17√2
(c)3:(34−12√2)
(d)None of these
View SolutionIf the refractive index of diamond is 2.4 find the velocity of light in diamond.(c=3×108m/s)
View Solution