If W1:W2=2:3 and W1:W3=1:2 the W2:W3 is 3:4 b. 4:3 c. 2:3 d. 4:5
To solve the problem, we need to find the ratio W2:W3 given the ratios W1:W2=2:3 and W1:W3=1:2.
1. Express the Ratios in Fraction Form:
- From the ratio W1:W2=2:3, we can express this as:
W1W2=23
- From the ratio W1:W3=1:2, we can express this as:
W1W3=12
2. Set Up the Equation:
- We want to find the ratio W2:W3. We can use the two fractions we have:
W2W3=W2W1×W1W3
3. Substituting the Values:
- We know that:
W1W2=23⟹W2W1=32
- Now substitute this into our equation:
W2W3=32×12
4. Calculate the Ratio:
- Multiply the fractions:
W2W3=3×12×2=34
5. Express the Result as a Ratio:
- This means:
W2:W3=3:4
Final Answer:
The ratio W2:W3 is 3:4.
- From the ratio W1:W2=2:3, we can express this as:
W1W2=23
- From the ratio W1:W3=1:2, we can express this as:
W1W3=12
- We want to find the ratio W2:W3. We can use the two fractions we have:
W2W3=W2W1×W1W3
- We know that:
W1W2=23⟹W2W1=32
- Now substitute this into our equation:
W2W3=32×12
- Multiply the fractions:
W2W3=3×12×2=34
- This means:
W2:W3=3:4
The ratio W2:W3 is 3:4.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If W1:W2=2:3 and W1:W3=1:2, then W2:W3 is:
A3:4B4:3C2:3D4:5If W1:W2=2:3 and W1:W3=1:2 then W2:W3 is
A3:4B4:3C2:3D4:5If i1=3sinωtand(i2)=4cosωt, then (i3) is
 A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)
A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)
Which of the following cannot be valid assignment of probability for elementary events or outcomes of samples space S={w1,w2,w3,w4,w5,w6,w7}: Elementary events w1 w2 w3 w4 w5 w6 w7 i. 0.1 0.01 0.05 0.03 0.01 0.2 0.6 ii. 17 17 17 17 17 17 17 iii. 0.7 0.6 0.5 0.4 0.3 0.2 0.1 iv. 114 214 314 414 514 614 1514
View SolutionIf w is a complex cube root of unity, then value of =∣∣a1+b1wa1w2+b1c1+b1wa2+b2wa2w2+b2c2+b2wa3+b3wa3w2+b3c3+b3w∣∣ is a. 0 b. −1 c. 2 d. none of these
View SolutionIf W : 0. 80 :: 9 : 6, W = ?
A. 2.5
B. 1.1
C. 3.3
D . 1.2
View SolutionA 100 W bulb B1, and two 60 W bulb B2 and B3, are connected to a 250 V source, as shown in figure. Now W1,W2andW3 are the output powers of the bulbs B1,B2andB3, respectively. Then
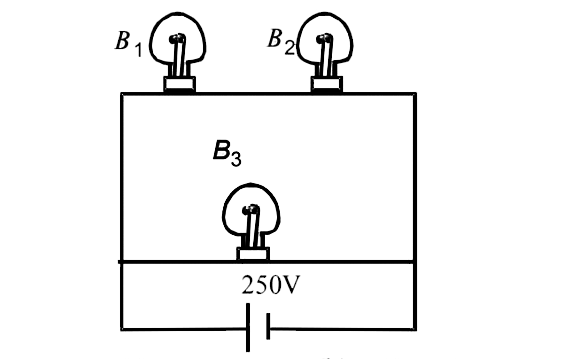
View SolutionA 100 W bulb B1, and two 60 W bulb B2 and B3, are connected to a 250 V source, as shown in figure. Now W1,W2andW3 are the output powers of the bulbs B1,B2andB3, respectively. Then

View Solution
