If a:b=c:d then ma+ncmb+nd is equal to m:n b. d:cn c. an:mb d. a:b
To solve the problem, we start with the given ratio:
1. Given: a:b=c:d
This implies that:
ab=cd
2. We need to find:
ma+ncmb+nd
3. Substituting the ratios:
Since a:b=c:d, we can express a and c in terms of b and d:
a=kbandc=kd
where k is a constant ratio.
4. Substituting into the expression:
Now, substituting a and c into the expression:
ma+ncmb+nd=m(kb)+n(kd)mb+nd
5. Factoring out k:
This simplifies to:
k(mb+nd)mb+nd
6. Canceling out the common terms:
The mb+nd in the numerator and denominator cancels out:
=k
7. Relating back to the original ratio:
Since k=ab or cd, we can express the result in terms of the original ratios:
=aborcd
8. Final Result:
Therefore, we conclude that:
ma+ncmb+nd=ab
Thus, the answer is:
Option d: a:b
---
ab=cd
ma+ncmb+nd
Since a:b=c:d, we can express a and c in terms of b and d:
a=kbandc=kd
where k is a constant ratio.
Now, substituting a and c into the expression:
ma+ncmb+nd=m(kb)+n(kd)mb+nd
This simplifies to:
k(mb+nd)mb+nd
The mb+nd in the numerator and denominator cancels out:
=k
Since k=ab or cd, we can express the result in terms of the original ratios:
=aborcd
Therefore, we conclude that:
ma+ncmb+nd=ab
Option d: a:b
Topper's Solved these Questions
Similar Questions
Knowledge Check
If ab=cd=ef=4, then
m2a+n2c+p2em2b+n2d+p2f=?A1B4C8D16
If A+B+C=180∘ , then tanA+tanB+tanCtanA tanB tanC is equal to tanAtanBtanC b. 0 c. 1 d. none of these
View SolutionIf m,n∈Nandm2−n2=13,then(m+1)(n+1) is equal to a. 42 b. 56 c. 50 d. none of these
View Solution7 lf If log (x y m 2n and log (x4 y n 2m, then log X is equal to (A) (B) m-n (c) men (D) m n
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View SolutionIf a and b are two numbers such that ab = 0 , then (a)a = 0 and b = 0 (b) a = 0 or b = 0 (c) a = 0 and b≠0 (d) b = 0 and a≠0
View SolutionRoots of the equation |xmn1axn1abx1abc1|=0 are independent of m,andn independent of a,b,andc depend on m,n,anda,b,c independent of m,nanda,b,c
View SolutionIn Figure, if AC is bisector fo ∠BAD such that AB=3 cm and AC=5 cm, then CD= 2 cm (b) 3 cm (c) 4 cm (d) 5 cm
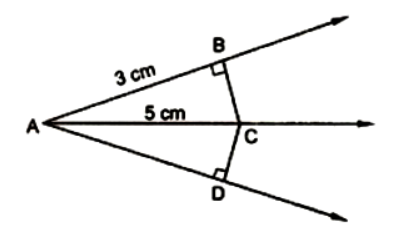
View Solution