The ratio of boys and girls in sections A, B, C and D of class VI is especially. 7:5, 5:3, 3:2 and 2:1. If the number of students in each of the sections is equal then maximum number of bys are enrolled in section A b. B c. C d. D
To solve the problem, we need to determine the maximum number of boys enrolled in each section (A, B, C, and D) based on the given ratios of boys to girls.
1. Identify the Ratios:
- Section A: Boys to Girls = 7:5
- Section B: Boys to Girls = 5:3
- Section C: Boys to Girls = 3:2
- Section D: Boys to Girls = 2:1
2. Express Boys and Girls in Terms of a Common Variable:
- Let the common variable for section A be u:
- Boys in A = 7u
- Girls in A = 5u
- For section B, let the common variable be x:
- Boys in B = 5x
- Girls in B = 3x
- For section C, let the common variable be y:
- Boys in C = 3y
- Girls in C = 2y
- For section D, let the common variable be z:
- Boys in D = 2z
- Girls in D = 1z
3. Set Up the Total Number of Students:
Since the total number of students in each section is equal, we can set up the equation based on the total number of students:
Total students in A=7u+5u=12u
Total students in B=5x+3x=8x
Total students in C=3y+2y=5y
Total students in D=2z+1z=3z
Therefore, we have:
12u=8x=5y=3z
4. Express Each Variable in Terms of a Common Variable k:
Let k be a common multiple:
- From 12u=k → u=k12
- From 8x=k → x=k8
- From 5y=k → y=k5
- From 3z=k → z=k3
5. Calculate the Number of Boys in Each Section:
- Boys in Section A:
7u=7(k12)=7k12
- Boys in Section B:
5x=5(k8)=5k8
- Boys in Section C:
3y=3(k5)=3k5
- Boys in Section D:
2z=2(k3)=2k3
6. Convert Each Expression to a Common Denominator:
To compare the number of boys, we convert each fraction to a common denominator:
- For Section A:
7k12=7k12
- For Section B:
5k8=15k24
- For Section C:
3k5=14.4k24
- For Section D:
2k3=16k24
7. Compare the Number of Boys:
- Section A: 7k12=14k/24
- Section B: 15k24
- Section C: 14.4k24
- Section D: 16k24
The maximum number of boys is in Section D.
Conclusion:
The maximum number of boys are enrolled in Section D.
- Section A: Boys to Girls = 7:5
- Section B: Boys to Girls = 5:3
- Section C: Boys to Girls = 3:2
- Section D: Boys to Girls = 2:1
- Let the common variable for section A be u:
- Boys in A = 7u
- Girls in A = 5u
- For section B, let the common variable be x:
- Boys in B = 5x
- Girls in B = 3x
- For section C, let the common variable be y:
- Boys in C = 3y
- Girls in C = 2y
- For section D, let the common variable be z:
- Boys in D = 2z
- Girls in D = 1z
Since the total number of students in each section is equal, we can set up the equation based on the total number of students:
Total students in A=7u+5u=12u
Total students in B=5x+3x=8x
Total students in C=3y+2y=5y
Total students in D=2z+1z=3z
Therefore, we have:
12u=8x=5y=3z
Let k be a common multiple:
- From 12u=k → u=k12
- From 8x=k → x=k8
- From 5y=k → y=k5
- From 3z=k → z=k3
- Boys in Section A:
7u=7(k12)=7k12
- Boys in Section B:
5x=5(k8)=5k8
- Boys in Section C:
3y=3(k5)=3k5
- Boys in Section D:
2z=2(k3)=2k3
To compare the number of boys, we convert each fraction to a common denominator:
- For Section A:
7k12=7k12
- For Section B:
5k8=15k24
- For Section C:
3k5=14.4k24
- For Section D:
2k3=16k24
- Section A: 7k12=14k/24
- Section B: 15k24
- Section C: 14.4k24
- Section D: 16k24
The maximum number of boys are enrolled in Section D.
Topper's Solved these Questions
Similar Questions
The given pictograph represents the number of students in 5 sections of class VI.

Study the given pictograph and answer the following questions.
Find the difference between the number of students in section E and the total number of students in section C and D together.
View SolutionThe ratio of boys and girls in a school is 12:5. If there are 840 girls in the school, then the number of boys is 1190 (b) 2380 (c) 2856 (d) 2142
View Solution
Knowledge Check
There are three sections A, B and C in class VIII of a school. The ratio of the number of students in A, B and C is 2:3:4. The section which has neither the maximum number of students has a strength of 30. Find the total strength of the three sections.
A63B81C72D90Read the data given below and answer the questions based on it.
There were 3 sections namely A, B and C in a test. Out of three 33 students passed in section A, 34 students passed in Section B and 32 passed in Section C. 10 students passed in Section A and Section B, 9 passed in Section B and Section C, 8 passed in Section A and Section C. The number of students who passed each section alone was equal and was 21 for each section.
The ratio of the number of students passed in one or more of the sections to the number of students who passed in section A alone is :
A. 78/21
B. 3
C. 73/21
D. 75/21ABBDCCDAThe total number of students in sections A and B ofa class is 72. The ratio of the number of students in A and B is 7: 5. The average weight(in kg) of the students in section B is 20% more than that of the studentsin section A.If the average weight of all the students in the class is 52 kg, then whatis the average weight (in kg) of the students in section B?
A58.2B57.9C57.6D56.4
The pie chart given below shows the number of students in 5 sections .The number of students is 7200.
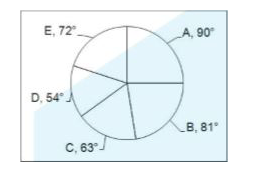
What is the total number of students in section E and section B?
View SolutionRead the data given below and answer the quesitons based on it.
There were 3 sections namely A, B and C in a test. Out of three sections, 33 passed section A, 34 students passed in Section B and 32 passed in Section C. 10 students passed in Section A and Section B, 9 passed in Section B and Section C, 8 passed in Section A and Section C. The number of students who passed each seciton alone was equal and was 21 for each section.
How many passed all the three sections ?
A. 3
B. 6
C. 5
D. 7
View SolutionDirection: Read the data given below and answer the question based on it. There were 3 sections namely A, B and C in a test. Out of three sections, 33 students passed in Section A, 34 students passed in Section B and 32 passed in Section C. 10 students passed in Section A and Section B, 9 passed in Section B and Section C, 8 passed in Section A and Section C. The number of students who passed each section alone was equal and was 21 for each section.How many passed only one of the three sections ?
A. 21
B. 42
C. 63
D. 52
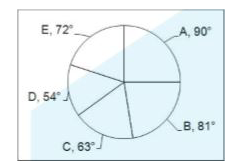
View SolutionThe pie chart given below shows the number of students in 5 sections .The number of students is 7200.
The number of students in section A is what percent of that of section B?

View SolutionThe pie chart given below shows the number of students in 5 sections .The number of students is 7200.
What is the difference between the number of students in section C and section D?
View Solution
