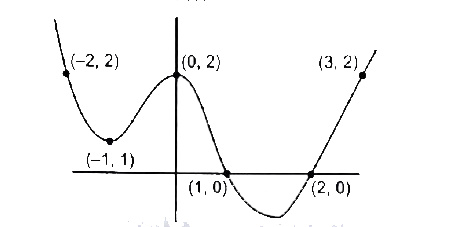
In the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
The product of all imaginery roots of p(x)=(0) is
1
2
1/3
1/4
The correct Answer is:A
(a) 1.2(α+iβ)(α−iβ)=p(0)=2⇒(α+iβ)(α−iβ)=1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer6videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Comprehension12videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
If x2+x+1 is a factor of ax3+bx2+cx+d, then the real root of ax3+bx2+cx+d=0 is
A−d/aBd/aCa/dDnone of these - Question 2 - Select One
If roots of the equation x4−8x3+bx2+cx+16=0 are positive, then
Ab=8=cBb=−24,c=−32Cb=24,c=−32Db=24,c=32
In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
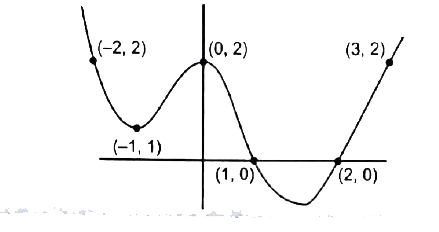
The minimum number of real roots of equation (p'(x))2+p(x)p''(x)=0 are:View SolutionIf P(x)=x4+ax3+bx2+cx+d,P(1)=P2=P(3)=0 then find P(4)
View SolutionIt is given that the graph of y=x4+ax3+bx2+cx+d (where a,b,c,d are real) has at least 3 points of intersection with the x-axis. Prove that either there are exactly 4 distinct points of intersection or one of there 3 point of intersection is a local minimum or meximum.
View SolutionLet α,β,γ are the roots of f(x)≡ax3+bx2+cx+d=0.Then The condition for the product of two of the roots is-1 is
View SolutionLet α,β,γ are the roots of (x)≡ax3+bx2+cx+d=0Then The condition for roots of f(x)=0 are in G.Pis
View SolutionLet α,β,γ are the roots of f(x)≡ax3+bx2+cx+d=0 . Then the condition for roots of f(x)=0 are in G.P is
(A) ac3=b3d
(B) a3c=bd3
(C) ac=bd
(D) a2c=b2dView Solution