The locus of any point $P (z)$ on argand plane is $a r g (\frac{z - 5 i}{z + 5 i}) = \frac{π}{4}$ .
Then the length of the arc described by the locus of $P (z)$ is

A

$10 \sqrt{2} π$

B

$\frac{15 π}{\sqrt{2}}$

C

$\frac{5 π}{\sqrt{2}}$

D

$5 \sqrt{2} π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$(b)$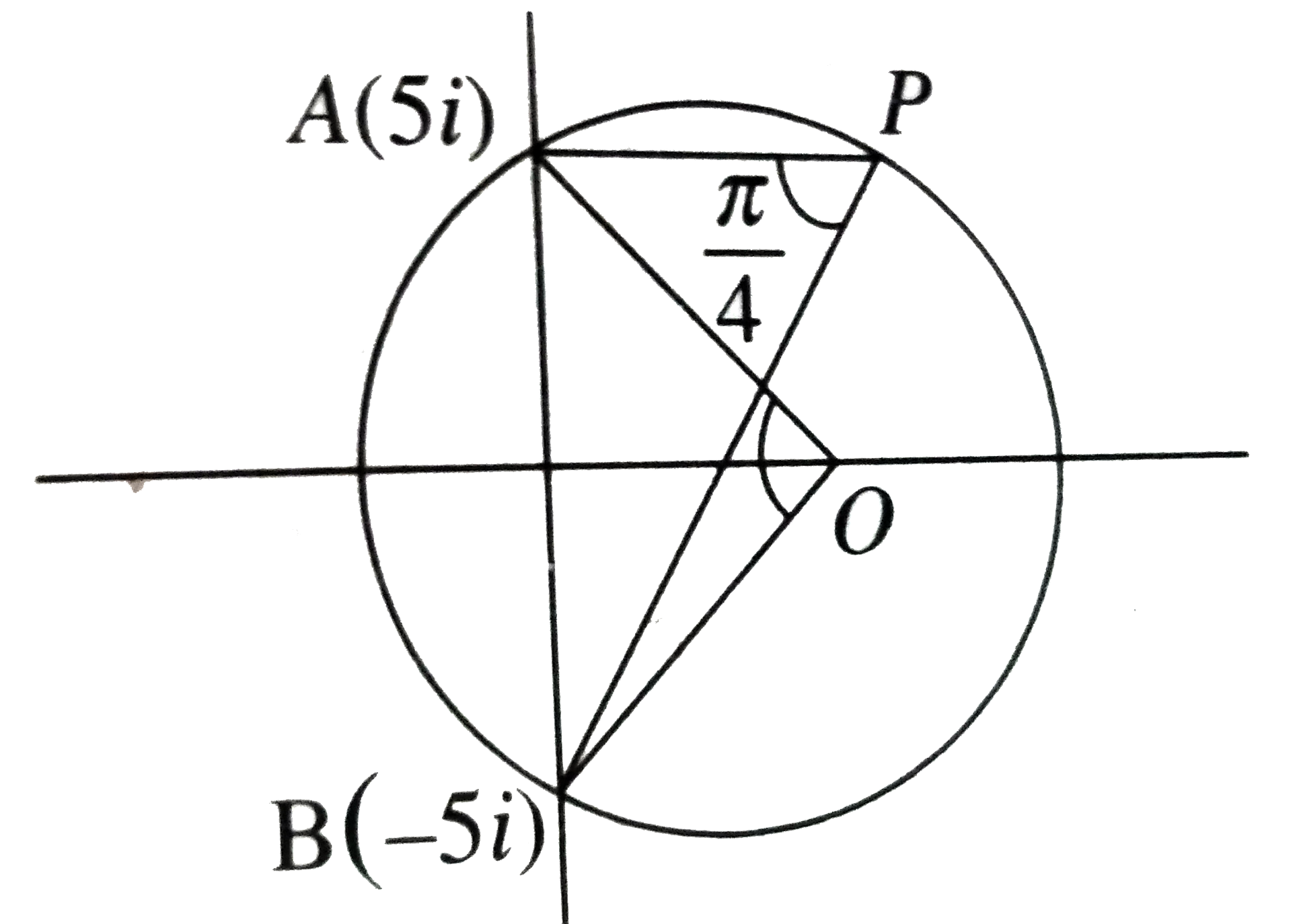
Given $∠ A P B = π / 4 \Rightarrow ∠ A O B = π / 2$
Let $O A = O B = R =$ radius of the circle
$\Rightarrow 2 R^{2} = 10^{2} \Rightarrow R = 5 \sqrt{2}$
Length of the arc $= 5 \sqrt{2} \times \frac{3 π}{2}$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The locus of any point $P (z)$ on argand plane is $a r g (\frac{z - 5 i}{z + 5 i}) = \frac{π}{4}$ .
Area of the region bounded by the locus of a complex number $Z$ satisfying $a r g (\frac{z + 5 i}{z - 5 i}) = \pm \frac{π}{4}$
A $75 π + 50$
B $75 π$
C $\frac{75 π}{2} + 25$
D $\frac{75 π}{2}$
Question 2 - Select One
The locus of any point P (z) on argand plane is $arg (\frac{z + 5 i}{z - 5 i}) = π / 4$ , then
Area of the region bounded by the locus of a complex number Z satisfying $(\frac{z + 5 i}{z - 5 i}) = \pm \frac{π}{4}$
A $75 π + 50$
B $75 π$
C $\frac{75 π}{2} + 25$
D $\frac{75 π}{2}$
Question 3 - Select One
The locus of any point $P (z)$ on argand plane is $a r g (\frac{z - 5 i}{z + 5 i}) = \frac{π}{4}$ .
Total number of integral points inside the region bounded by the locus of $P (z)$ and imaginery axis on the argand plane is
A $62$
B $74$
C $136$
D $138$

CENGAGE-COMPLEX NUMBERS-Comprehension

Home
Ask Doubt
Profile