The locus of any point P(z) on argand plane is arg(z−5iz+5i)=π4.
Area of the region bounded by the locus of a complex number Z satisfying arg(z+5iz−5i)=±π4
75π+50
75π
75π2+25
75π2
The correct Answer is:A
(a) 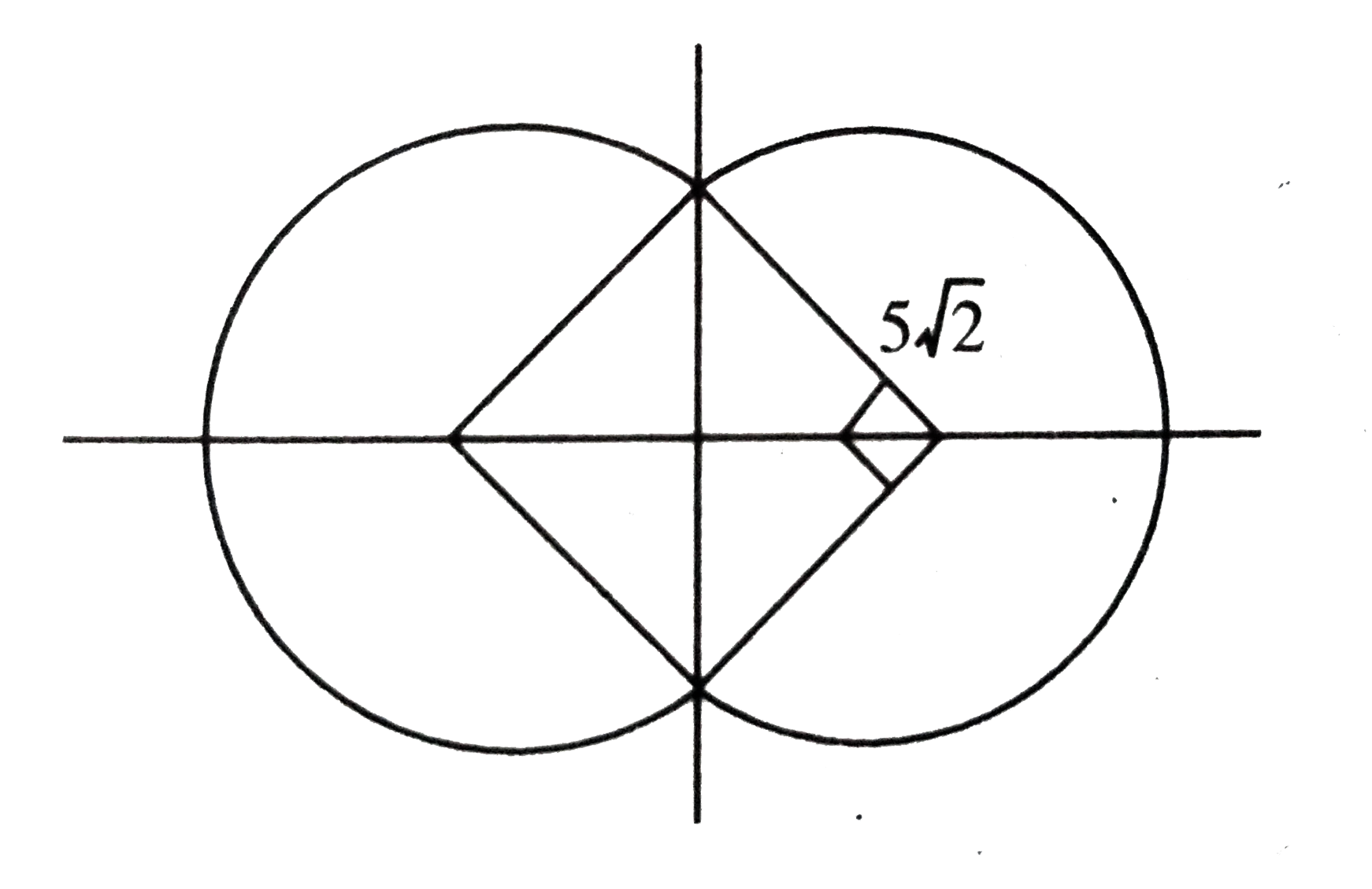
Required are =2[12×(5√2)2+12(5√2)2×3π2]
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Examples
125 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Exercise 3.1
4 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
91 Videos
Similar Questions
The locus of any point P(z) on argand plane is arg(z−5iz+5i)=π4.
Then the length of the arc described by the locus of P(z) is
View SolutionThe locus of any point P(z) on argand plane is arg(z−5iz+5i)=π4.
Total number of integral points inside the region bounded by the locus of P(z) and imaginery axis on the argand plane is
View Solution
Knowledge Check
The locus of any point P (z) on argand plane is arg(z+5iz−5i)=π/4, then
Area of the region bounded by the locus of a complex number Z satisfying (z+5iz−5i)=±π4A75π+50B75πC75π2+25D75π2The locus of any point P(z) on argand plane is arg(z−5iz+5i)=π4.
Then the length of the arc described by the locus of P(z) isA10√2πB15π√2C5π√2D5√2πThe locus of any point P(z) on argand plane is arg(z−5iz+5i)=π4.
Total number of integral points inside the region bounded by the locus of P(z) and imaginery axis on the argand plane isA62B74C136D138
Let the locus of any point P(z) in the argand plane is arg(z−5iz+5i)=π4. If O is the origin, then the value of max.(OP)+min.(OP)2 is
View SolutionIf arg(z−2z+2)=π4 then the locus of z is
View SolutionComplex number z lies on the curve S≡arg(z+3)z+3i=−π4
View SolutionFind the locus of the complex number z=x+iy, satisfying relations arg(z−1)=π4 and |z−2−3i|=2.
View SolutionLet the locus of any point P(z) in the argand plane is arg(z−5iz+5i)=π4. If O is the origin, then the value of max.(OP)+min.(OP)2 is
View Solution
