A bus stop is barricaded from the remaining part of the road, by using 50 hollowcones made of recycled cardboard. Each cone has a base diameter of 40 cm and height1 m. If the outer side of each of the cones is to be painted and the cost of pain
To solve the problem step by step, we will follow the outlined process below:
Step 1: Understand the dimensions of the cone
- Given:
- Diameter of the cone = 40 cm
- Height of the cone = 1 m
Step 2: Convert the diameter to radius and height to the same unit
- Radius (R) = Diameter / 2 = 40 cm / 2 = 20 cm = 0.2 m (since 1 m = 100 cm)
- Height (H) = 1 m
Step 3: Calculate the slant height (L) of the cone
- Use the Pythagorean theorem to find the slant height:
L=√H2+R2
L=√(1)2+(0.2)2=√1+0.04=√1.04≈1.02m
Step 4: Calculate the curved surface area (CSA) of one cone
- The formula for the curved surface area of a cone is:
CSA=πRL
- Substituting the values:
CSA=227×0.2×1.02≈0.64046m2
Step 5: Calculate the cost of painting one cone
- Given the cost of painting is ₹12 per m²:
Cost for one cone=CSA×Cost per m2
Cost for one cone=0.64046×12≈7.68552₹
Step 6: Calculate the total cost for 50 cones
- Total cost for 50 cones:
Total Cost=50×Cost for one cone
Total Cost=50×7.68552≈384.34₹
Final Answer
The total cost of painting the outer side of 50 cones is approximately ₹384.34.
---
- Given:
- Diameter of the cone = 40 cm
- Height of the cone = 1 m
- Radius (R) = Diameter / 2 = 40 cm / 2 = 20 cm = 0.2 m (since 1 m = 100 cm)
- Height (H) = 1 m
- Use the Pythagorean theorem to find the slant height:
L=√H2+R2
L=√(1)2+(0.2)2=√1+0.04=√1.04≈1.02m
- The formula for the curved surface area of a cone is:
CSA=πRL
- Substituting the values:
CSA=227×0.2×1.02≈0.64046m2
- Given the cost of painting is ₹12 per m²:
Cost for one cone=CSA×Cost per m2
Cost for one cone=0.64046×12≈7.68552₹
- Total cost for 50 cones:
Total Cost=50×Cost for one cone
Total Cost=50×7.68552≈384.34₹
The total cost of painting the outer side of 50 cones is approximately ₹384.34.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.93videos
SURFACE AREAS AND VOLUMES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.79videos
SURFACE AREAS AND VOLUMES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.810videos
SURFACE AREAS AND VOLUMES
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.12videos
STATISTICS
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.28videos
TRIANGLES
Similar Questions
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled card-board. Each cone has a base diameter of 40cm and height 1m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m2 , what will be the cost of painting all these cones (Useπ=3.14and√1.04=1.02))
View SolutionA bus stop is barricated from the remaining part of the road by using 50 hollow cones made of recycled cardboard. Each one has a base diameter of 40 cm and height 1m. If the outer side of each of the cones is to be painted and the cost of painting is Rs 25 per m2, what will be the cost of painting all these cone ? (Use π=3.14and√1.04=1.02)
View Solution
Knowledge Check
- Question 1 - Select One
In a toys manufacturing company, wooden parts are assembled and painted to prepare a toy. One specific toy is in the shape of a cone mounted on a cylinder.
For the wood processing activity center, the wood is taken out of storage to be sawed, after which it undergoes rough polishing, then is cut, drilled and has holes punched in it. It is then fine polished using sandpaper.

For the retail packaging and delivery activity center, the polished wood sub-parts are assembled together, then decorated using paint.
The total height of the toy is 26 cm and the height of its conical part is 6 cm. The diameters of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm.
If its conical part is to be painted green, the surface area need to be painted isA26.6π sq cmB22.5π sq cmC20.5π sq cmD18.5π sq cm
A bus stop is barricaded from the remaining part of the road, by using 50 hollowcones made of recycled cardboard. Each cone has a base diameter of 40 cm and height1 m. If the outer side of each of the cones is to be painted and the cost of pain
View SolutionOn a construction site, a deep pit is barricaded from the remaining portion by asing 100 hollow cones made of recycled plastic.Each one has a base diameter 20 cm and height half a meter. What is the cost of paining all the cones,if the outerside of each cone is to be painted red and cost of paining is rs30m2
View SolutionA wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in figure. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical partition has a diameter of 5 cm, while the base diameter of the cylindrical protion is 3 cm.
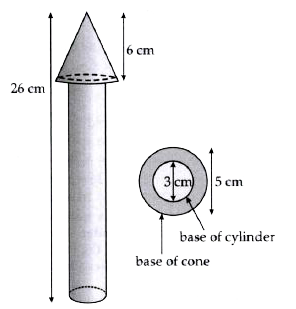
If the conical portion is to be painted orange, find the area to be painted orange. Find the area of the rockeeet peainted with each of these colours? (Take π = 3.14)View SolutionA wooden toy rocket is in the shape of a cone mounted on a cylinder. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours.
View SolutionA wooden toy rocket is in the shape of a cone mounted on a cylinder as shown in Fig. 16.36. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π=3.14 )
View Solution12 solid spheres of the same size are made by melting a solid metallic cone of base radius 1 cm and height of 48 cm. Find the radius of each sphere.
View SolutionHanumappa and his wife Gangavva are busy making Jaggery out of sugar-cane. They have processed the sugarcane juice to make the molasses which is poured into moulds of the shape shown in Fig 16.72. It will be cooled to solidify in this shape to be sent to the market. Each mould is in the sh ape of a frustum of a cone having the diameters of its two circular ends as 30 cm and 35 cm and the height of the mould is 14 cm. If each cm3 of molasses weighs about 1.2 gm, find the weight of molasses that can be poured into each mould (Take π=22/7 )
View Solution

