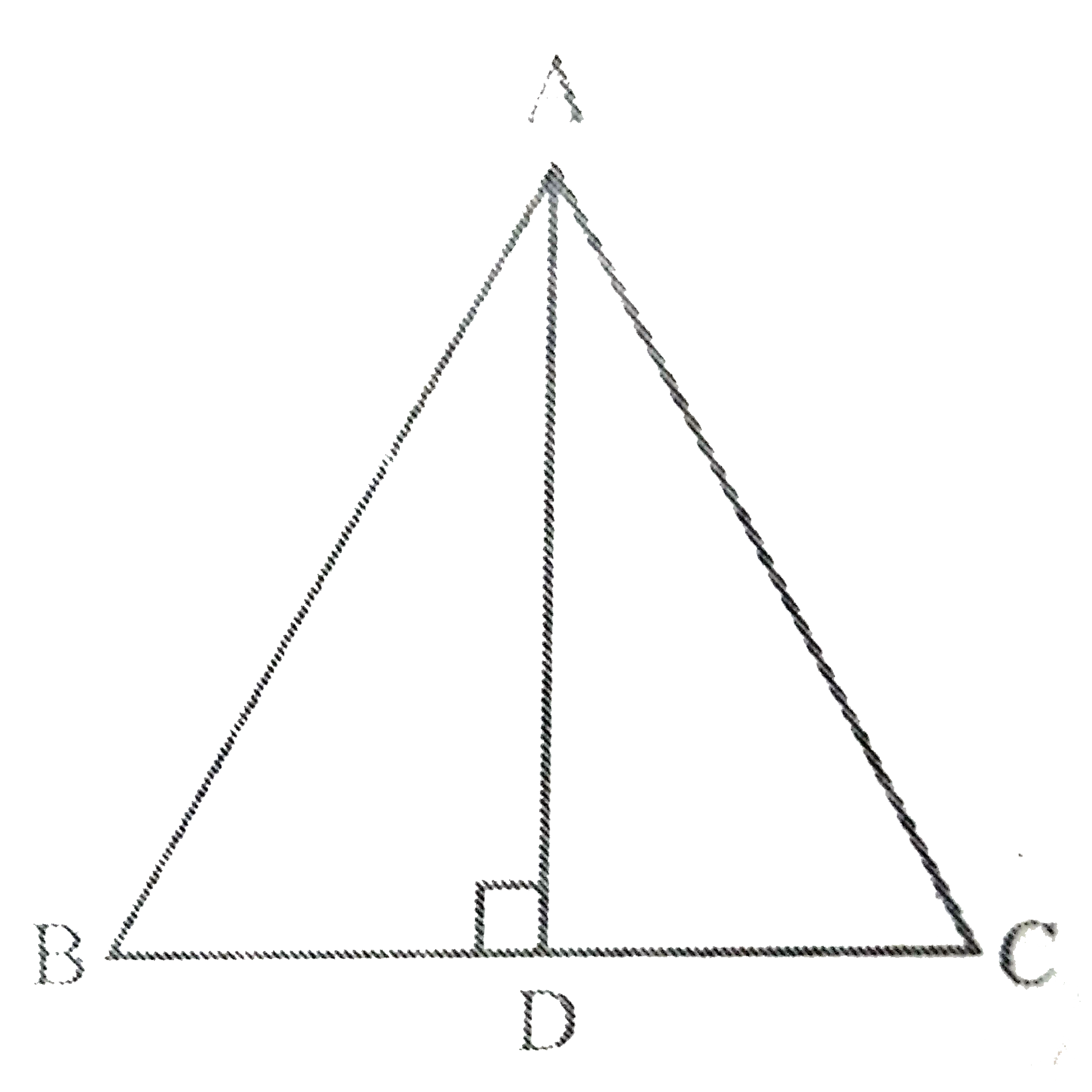
In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
Video Solution
Text Solution

Given: AD is the perpendicular bisector of BC means ∠ADB=∠ADC=90∘ and BD=DC
To Prove: ΔABC is an isosceles triangle in which AB=AC.
In ΔADC and ΔADB,
AD=AD (Common)
∠ADC=∠ADB (Each 90∘)
CD=BD (AD is the perpendicular bisector of BC)
∴ΔADC≅ΔADB (By SAS congruence rule)
∴AB=AC (By CPCT)
Therefore, ABC is an isosceles triangle in which AB=AC.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoning figure of ΔABC,AD is the perpendicular bisector of side BC. The triangle ABC is :
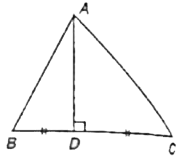 Aright angledBisoscelesCscaleneDequilateral
Aright angledBisoscelesCscaleneDequilateral - Question 2 - Select One
In triangle ABC, AD is prependicular to BC and DE is perpendicular to AB
 AabcdprqqBabcdqrpsCabcdspqrDabcdrpsq
AabcdprqqBabcdqrpsCabcdspqrDabcdrpsq - Question 3 - Select One
In a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
A10B12C14D√221
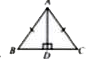
In ⋀ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
AD bisects BCView SolutionIn ΔABC, if cosAa=cosBb, then show that it is an isosceles triangle.
View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionIn ΔABC,ADandBE are perpendiculars from A and B to the sides BC and AC, then
View Solution

