A water jet from a function reaches it maximum height of 4 m at a distance 0.5 m from the vertical passing through the point O of water outlet. The height of the jet above the horizontal OX at a distance of 0.75 m from the point O is 5 m (b) 6 m (c) 3 m (d) 7 m
To solve the problem, we need to find the height of the water jet at a distance of 0.75 m from the point O, given that the maximum height of the jet is 4 m at a distance of 0.5 m.
1. Understanding the Problem:
The water jet follows a parabolic path, reaching its maximum height at a specific point. We will model the height of the jet using a quadratic equation.
2. Setting Up the Coordinate System:
Let point O be the origin (0, 0). The maximum height of 4 m occurs at a horizontal distance of 0.5 m from O. Therefore, we can denote this point as (0.5, 4).
3. Formulating the Parabola:
Since the maximum height occurs at x = 0.5, we can express the height y as a function of x in the form:
y=a(x−0)(x−1)
This can be simplified to:
y=ax(x−1)
The roots of this parabola are at x=0 and x=1.
4. Finding the Value of a:
We know that at x=0.5, y=4. Plugging these values into the equation:
4=a(0.5)(0.5−1)
Simplifying this gives:
4=a(0.5)(−0.5)⟹4=−0.25a⟹a=−16
5. Final Equation of the Parabola:
Now we can write the equation of the parabola:
y=−16x(x−1)=−16x2+16x
6. Calculating the Height at x=0.75:
We need to find the height of the jet at x=0.75:
y=−16(0.75)2+16(0.75)
Calculating (0.75)2=0.5625:
y=−16(0.5625)+12=−9+12=3
7. Conclusion:
The height of the jet above the horizontal line OX at a distance of 0.75 m from point O is 3 m.
Final Answer:
(c) 3 m
The water jet follows a parabolic path, reaching its maximum height at a specific point. We will model the height of the jet using a quadratic equation.
Let point O be the origin (0, 0). The maximum height of 4 m occurs at a horizontal distance of 0.5 m from O. Therefore, we can denote this point as (0.5, 4).
Since the maximum height occurs at x = 0.5, we can express the height y as a function of x in the form:
y=a(x−0)(x−1)
This can be simplified to:
y=ax(x−1)
The roots of this parabola are at x=0 and x=1.
We know that at x=0.5, y=4. Plugging these values into the equation:
4=a(0.5)(0.5−1)
Simplifying this gives:
4=a(0.5)(−0.5)⟹4=−0.25a⟹a=−16
Now we can write the equation of the parabola:
y=−16x(x−1)=−16x2+16x
We need to find the height of the jet at x=0.75:
y=−16(0.75)2+16(0.75)
Calculating (0.75)2=0.5625:
y=−16(0.5625)+12=−9+12=3
The height of the jet above the horizontal line OX at a distance of 0.75 m from point O is 3 m.
(c) 3 m
Similar Questions
A water jet from a function reaches it maximum height of 4 m at a distance 0.5 m from the vertical passing through the point O of water outlet. The height of the jet above the horizontal OX at a distance of 0.75 m from the point O is 5 m (b) 6 m (c) 3 m (d) 7 m
View SolutionA pin hole camera of which 1 m is focussed to an object at a distance 30 m from it. If the height of the object is 3 m, what is the height of the image? ltbgt
View Solution
Knowledge Check
A projectile rises to a height of 10 m and then falls at a distance of 30 m away from the projection. Its vertical displacement is
A0 mB5 mC6 mD7 mThe angle of elevation of the top of a tower of height 100√3m from a point at a distance of 100 m from the foot of the tower on a horizontal plane is
A60∘B90∘C120∘D180∘The angle of elevation of the top of a tower of height 100√3m from a point at a distance of 100 m from the foot of the tower on a horizontal plane is
A60∘B90∘C120∘D180∘
A tower of height 5m and a flagstaff on top of the tower subtend equal angles at a point on the ground, distance 13m from the base of the tower. The height of the flagstaff is
View SolutionHeight of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
View SolutionA ball thrown up from the ground reaches a maximum height of 20m Find:
a. Its initial velocity.
b. The time taken to reach the highest point.
c. Its velocity just before hitting the ground.
d. Its desplacement berween 0.5m above the ground.
View SolutionA body is thrown vertically upward from a point A 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through A on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is (g=10m/s2)
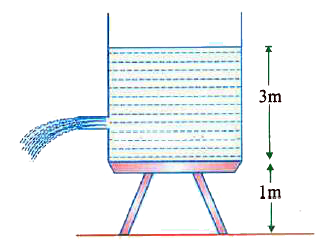
View SolutionWater is filled in tank 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
View Solution
