In the matrix A=⎡⎢
⎢
⎢
⎢
⎢⎣8943−1√7√325143068−111⎤⎥
⎥
⎥
⎥
⎥⎦, write
The order of the matrix.Solution in Tamil
Step by step video & image solution for In the matrix A=[(8, 9, 4, 3), (-1, sqrt(7), (sqrt(3))/(2), 5), (1, 4, 3, 0), (6, 8, -11, 1)], write The order of the matrix. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALGEBRABOOK - FULL MARKSCHAPTER - ALGEBRAEXERCISE - Exercise 3.17
8 Videos
- ALGEBRABOOK - FULL MARKSCHAPTER - ALGEBRAEXERCISE - Exercise 3.18
13 Videos
- ALGEBRABOOK - FULL MARKSCHAPTER - ALGEBRAEXERCISE - Exercise 3.15
8 Videos
- COORDINATE GEOMETRY BOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRY EXERCISE - ADDITIONAL QUESTIONS SOLVED (Answer the following questions)
20 Videos
Similar Questions
If A=⎡⎢⎣19348−3⎤⎥⎦,B=⎡⎢⎣573310⎤⎥⎦ then verify that
A+B=B+A
View SolutionFind the order of the product matrix AB is
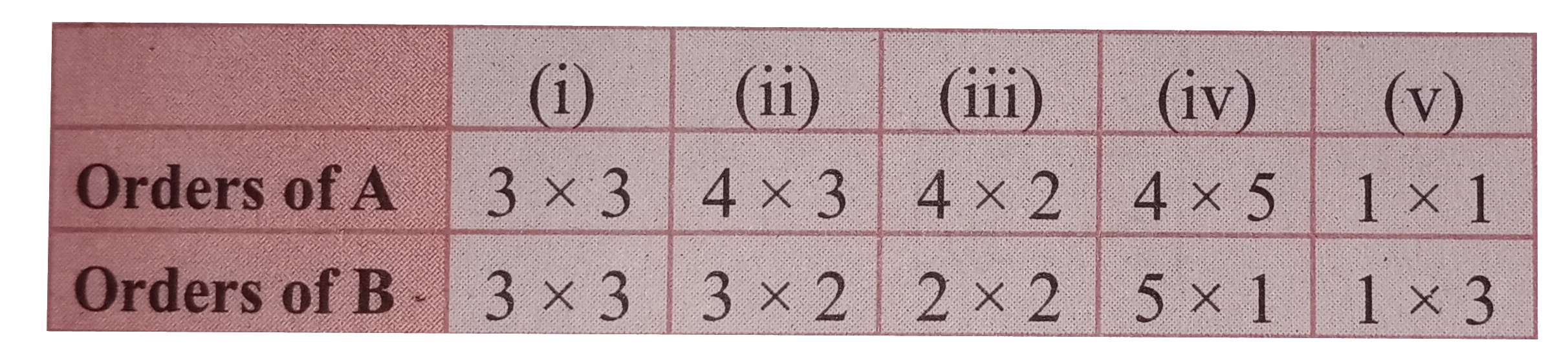
View SolutionGraph the following quadratic equations and state their nature of solutions.
x2+x+7=0
View SolutionIf the points (3,-4) (1,6) and (-2,3) are the vertices of a triangle ,find its area.
View Solution(1)/(1+sqrt(2))+(1)/(sqrt(2)+sqrt(3))+(1)/(sqrt(3)+sqrt(4))+(1)/(sqrt(4)+sqrt(5))+(1)/(sqrt(5)+sqrt(6))+(1)/(sqrt(6)+sqrt(7))+(1)/(sqrt(7)+sqrt(8))+(1)/(sqrt(8)+sqrt(9))
View SolutionProve that: 11+√2+1√2+√3+1√3+ √4+1√4+√5+1√5+√6+1√6+√7+ 1√7+√8+1√8+√9=2
View SolutionFind the matrix A such that : [1001]A=[335101]
View SolutionIf A=⎡⎢⎣20−3431−572⎤⎥⎦ is expressed as the sum of a symmetric and skew-symmetric matrix, then the symmetric matrix is (a) ⎡⎢⎣22−4234−442⎤⎥⎦ (b) ⎡⎢⎣24−5037−312⎤⎥⎦ (c) ⎡⎢⎣44−8468−884⎤⎥⎦ (d) ⎡⎢⎣100010001⎤⎥⎦
View Solutionआव्यूह X ज्ञात कीजिए , यदि X[123456]=[−7−8−9246] है |
View SolutionProve that (i) 13+√7+1√7+√5+1√5+√3+1√3+1=1 (ii) 11+√2+1√2+√3+1√3+√4+1√4+√5+1√5+√6+1√6+√7+1√7+√8+1√8+√9=2
View SolutionIn the matrix A=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣8943−1√7√325143068−111⎤⎥ ⎥ ⎥ ⎥ ⎥⎦, write
The number of elements.
View SolutionIn the matrix A=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣8943−1√7√325143068−111⎤⎥ ⎥ ⎥ ⎥ ⎥⎦, write
The order of the matrix.
View SolutionIn the matrix A=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣8943−1√7√325143068−111⎤⎥ ⎥ ⎥ ⎥ ⎥⎦, write
Write the elements a22,a23,a24,a34,a43,a44,
View SolutionFor the given matrix A=⎡⎢⎣135724689111315⎤⎥⎦ the order of the matrix AT is
View SolutionThe rank of the matrix
⎡⎢ ⎢ ⎢ ⎢⎣35−14213−281116−7−146−14⎤⎥ ⎥ ⎥ ⎥⎦
View SolutionFind the inverse of the matrix B=[40 −25]. Hence, find a matrix A such that, AB+[−1−9 36]=[37 168].
View Solution
