Construct a 3×3 matrix whose elements are given by
aij=(i+j)33Solution in Tamil
Step by step video & image solution for Construct a 3times3 matrix whose elements are given by a_(ij)=((i+j)^(3))/(3) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALGEBRABOOK - FULL MARKSCHAPTER - ALGEBRAEXERCISE - Exercise 3.17
8 Videos
- ALGEBRABOOK - FULL MARKSCHAPTER - ALGEBRAEXERCISE - Exercise 3.18
13 Videos
- ALGEBRABOOK - FULL MARKSCHAPTER - ALGEBRAEXERCISE - Exercise 3.15
8 Videos
- COORDINATE GEOMETRY BOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRY EXERCISE - ADDITIONAL QUESTIONS SOLVED (Answer the following questions)
20 Videos
Similar Questions
If A=⎡⎢⎣19348−3⎤⎥⎦,B=⎡⎢⎣573310⎤⎥⎦ then verify that
A+B=B+A
View SolutionFind the order of the product matrix AB is
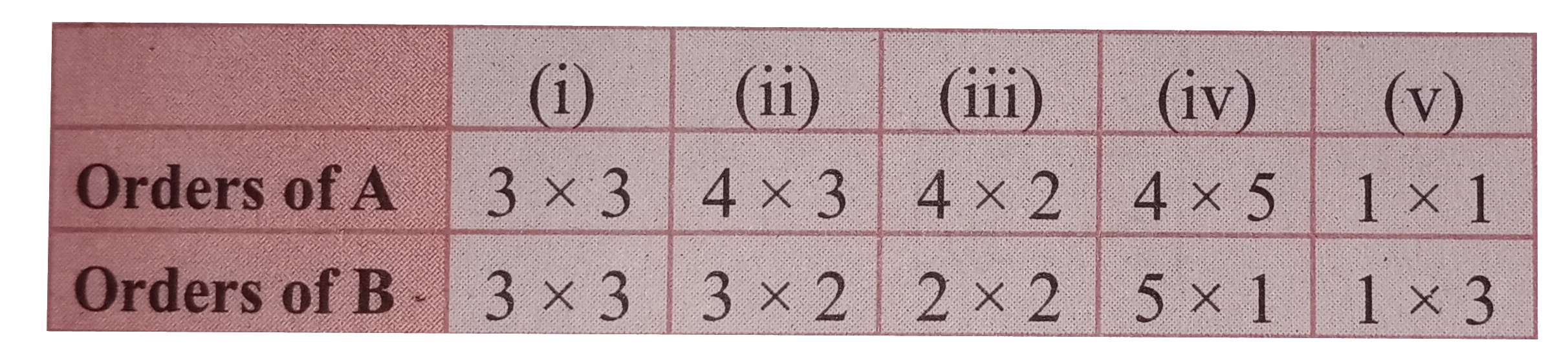
View SolutionGraph the following quadratic equations and state their nature of solutions.
x2+x+7=0
View SolutionIf the points (3,-4) (1,6) and (-2,3) are the vertices of a triangle ,find its area.
View Solutionconstruct 3^(*)4 matrix A=[a_(ij)] whose elements a_(ij) are given by: a_(ij)=|-3i+j|
View SolutionConstruct a 3×4 matrix A=[aij] whose elements are given by (i)aij=i+j (ii) aij=i−j
View SolutionConstruct a 2×3 matrix A=[aij] whose elements are given by aij=i−ji+j .
View SolutionConstruct a 4×3 matrix A=[aij] whose elements aij are given by: (i) aij=2i+ij
View SolutionConstruct 3×3 matrix whose elements are given by : aij=i−j
View SolutionConstruct 3×3 matrix whose elements are given by : aij=i+j
View SolutionConstruct a 3×3 matrix whose elements are given by
aij=|i−2j|
View SolutionConstruct a 3×3 matrix whose elements are given by
aij=(i+j)33
View SolutionConstruct a 3×4 matrix, A=[aij] whose elements are given by: (ii) aij=2i−j
View SolutionConstruct a 2×2 matrix A=[aij] whose elements are given by :
aij=2i−j3
View SolutionConstruct a 3×3 matrix A whose (i,j)th elements is aij=2i−j
View SolutionConstruct a 3×2 matrix A=[aij], whose elements are given by aij=⎧⎪⎨⎪⎩i−j,i<ji+j,i=ji⋅j,i>j.
View Solution
