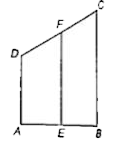
ABCD is a quadrilateral in which AB= AD, the bisector of ∠BACand∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.Solution in Tamil
Step by step video & image solution for ABCD is a quadrilateral in which AB= AD, the bisector of angle BAC and angle CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A Relation R is given by the set {(x,y)∣y=x+3,ξn{0,1,2,4,5}}. Determine its domain and range.
View SolutionDraw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.
View SolutionDraw the graph of y=x2+3x+2 and use it to solve x2+2x+1=0.
View SolutionABCD is a quadrilateral in which AB=AD . The bisector of BAC AND CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF||BD.
View SolutionIf ABCD is quadrilateral and EandF are the mid-points of ACandBD respectively, prove that →AB+→AD +→CB +→CD =4 →EF.
View SolutionIn the figure,AD is the bisector of angle BAC. Prove that AB>BD.
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View Solutionआकृति 6.63 में त्रिभुज ABC कि भुजा BC पर एक बिंदु D इस प्रकार स्तिथ हैं कि BDCD=ABAC हैं। स्तिथ कीजिये कि AD, कोण BAC का समद्विभाजक हैं।

View SolutionABCD is a cyclic quadrilateral .The side BC is extended to E .The bisectors of the angles ∠BADand∠DCE intersect at the point P .Prove that ∠ADC=∠APC .
View Solutionएक चतुर्भुज ABCD में AB =AD है| ∠BAC और ∠CAD के समद्विभाजक, चतुर्भुज की भुजाओं BC व CD को क्रमशः बिंदु E व F पर मिलते है|सिद्ध करो की EF∣∣BD
View Solutionएक चतुर्भुज ABCD में विकर्ण BD, ∠B और ∠D दोनों को समद्विभाजित करता है सिद्ध कीजिये कि ABBC=ADCD
View SolutionABCD is a quadrilateral in which AB= AD, the bisector of ∠BACand∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.
View SolutionIf ABCD is a quadrilateral and E and F are the midpoints of AC and BD respectively, then prove that −−→AB+−−→AD+−−→CB+−−→CD=4−−→EF.
View Solutionநாற்கரம் ABCD -யில் AB =AD .∠BAC மற்றும் ∠CAD யின் கோணம் இருசமவெட்டிகள் BC ,மற்றும் CD ஆகிய பக்கங்கள் முறையே E மற்றும் F என்ற புள்ளிகள் சந்திக்கிறன்றன .எனில் EF ||BD என் நிறுவுக ?
View SolutionABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
View SolutionABCD is a quadrilateral in which AB=BC and AD=CD ,Show that BD bisects both the ∠ABC and ∠ADC.
View Solution
