ABCD is a quadrilateral in which AB=AD . The bisector of BAC and CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF||BD.
Step by step video & image solution for ABCD is a quadrilateral in which AB=AD . The bisector of BAC and CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF||BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionABCD is a quadrilateral in which AB=BC and AD=CD ,Show that BD bisects both the ∠ABC and ∠ADC.
View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionIn the following figure , ABCD is a cyclic quadrilateral in which AD is parallel to BC .
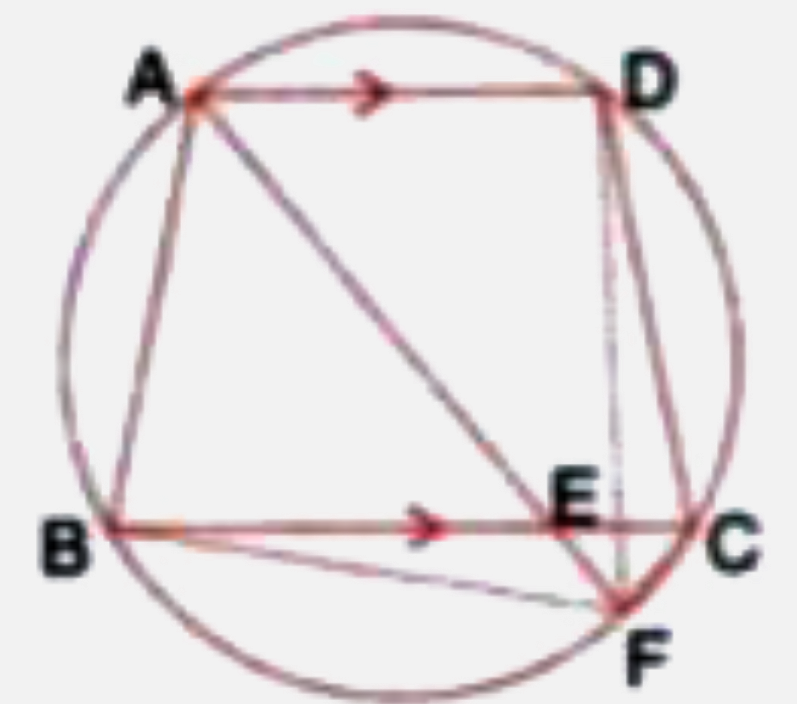
If the bisector of angle A meets BC at point E and given circle at point F, prove that :
(i) EF =FC
(ii) BF = DF
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionIn parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
triangle HEB and FHC are congruent.
View SolutionIn parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
GEHF is a parallelogram.
View Solution