Find the volume of the spherical cap of height h cut of feom a sphere of radius r.
Text Solution
The correct Answer is:13πh2(3r−h).
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRATIONBOOK - FULL MARKSCHAPTER - APPLICATIONS OF INTEGRATIONEXERCISE - EXERCISE 9.1
3 Videos
- APPLICATIONS OF INTEGRATIONBOOK - FULL MARKSCHAPTER - APPLICATIONS OF INTEGRATIONEXERCISE - EXERCISE 9.2
1 Videos
- APPLICATIONS OF DIFFERENTIAL CALCULUS BOOK - FULL MARKSCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUS EXERCISE - ADDITIONAL QUESTIONS SOLVED
56 Videos
- APPLICATIONS OF MATRICES AND DETERMINANTSBOOK - FULL MARKSCHAPTER - APPLICATIONS OF MATRICES AND DETERMINANTSEXERCISE - ADDITIONAL QUESTIONS SOLVED
56 Videos
Similar Questions
Knowledge Check
The volume of a spherical cap of height h cut off from a sphere of radius a is equal to :
Aπ3h2(3a−h)Bπ(a−h)(2a2−h2−ah)C4π3h2Dnone of the aboveThe volume of a spherical cap of height h cut off from a sphere of radius a is equal to :
Aπ3h2(3a−h)Bπ(a−h)(2a2−h2−ah)C4π3h2Dnone of the aboveThe volume of a sphere of radius 2r is
A32πr33B16πr33C8πr33D64πr33
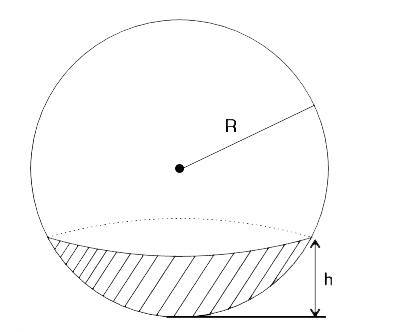
Show that the volume of a segment of height h of a sphere of radius R is
V=13πh2(3R−h)
View SolutionFind the volume of the largest cylinder that can be inscribed in a sphere of radius r
View SolutionA sphere of maximum volume is cut out from a solid hemisphere of radius r . The ratio of the volume of the hemisphere to that of the cut out sphere is: (a) 3 : 2 (b) 4 : 1 (c) 4 : 3 (d) 7 : 4
View SolutionA sphere of maximum volume is cut out from a solid hemisphere of radius r . The ratio of the volume of the hemisphere to that of the cut out sphere is: (a) 3 : 2 (b) 4 : 1 (c) 4 : 3 (d) 7 : 4
View SolutionFind the volume of a sector of a sphere, the radius 10 cm and height of the cap is 9 cm ?
View Solution
