If X is the random variable with distribution function F(x) given by , F(x) =⎧⎪⎨⎪⎩ox<0x0≤x<111≤x then find (i) the probability density function f(x) (ii) P(0.2≤X≤0.7) . Solution in Tamil
Step by step video & image solution for If X is the random variable with distribution function F(x) given by , F(x) ={(o,xlt0),(x,0lt=xlt1),(1,1lt=x):} then find (i) the probability density function f(x) (ii) P(0.2lt=Xlt=0.7) . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONSBOOK - FULL MARKSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE -11.1
5 Videos
- PROBABILITY DISTRIBUTIONSBOOK - FULL MARKSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE -11.2
7 Videos
- ORDINARY DIFFERENTIAL EQUATIONS BOOK - FULL MARKSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - ADDITIONAL PROBLEMS
40 Videos
- SAMPLE PAPER - 1 BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 1 EXERCISE - PART-IV (Answer the questions)
14 Videos
Similar Questions
Suppose X is the number of tails occurred when three fair coins are tossed once simultaneously. Find the values of the random variable X and number of points in its inverse images .
View SolutionThree fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
View SolutionFind the order and degree of the following differential equations
(i) dydx+y=x2
(ii) y'+y2=x
(iii) y'+3y2+y3=0
(iv) d2ydx2+x=√y+dydx
(v) d2ydx2−y+dydx+d3y(dx3)32=0
(vi)y'=(y−y'3)2/3
(vii)y'+(y2)=(x+y2)
(viiii)y'+(y)2=x(x+y)2 (ix)dy(dx)2+x=dxdy+x2
(x) sinx(dx+dy)=cosx(dx−dy)
View SolutionBy using Gaussian elimination method, balance the chemical reaction equation:
C2H6+O2→H2O+CO2.
View SolutionShow that the function f(x) defined by .f(x)=17, for 1≤x≤8 =0, otherwise, is a probability density function for a random variable. Hence find P(3<X<10)
View SolutionIf the probability density function of a random variable X is given as
then F(0) is equal to

View SolutionFind k if the function f(x) is defined by
f(x)=kx(1−x),for 0<x<1
=0 , otherwise, is the probability density function (p.d.f.) of a random varible (r.v) X. Also find P (X<12)
View SolutionIf X is the random variable with probability density function f(x) is given by
f(x)=⎧⎪⎨⎪⎩x+1−1≤x<0−x+10≤x<10otherwise
then find (i) the distribution function F(x) (ii) P(−0.5≤X≤0.5)
View SolutionIf X is the random varibale with distribution function F(x) given by
F(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩0−∞<x<032(x−x33)0≤x<113≤x<∞
Find probability density function f(x)
View SolutionIf the probability mass function f(x) of a random variable X is

find (i) its cumulative distribution hence find (ii) P (X ≤3) and , (iii) P(X≥2)
View SolutionFind the probability mass function f(x) of the discrete random variable X whose cumulative distribution function F(x) is given by F (x) = ⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0−∞<x<−20.25−2≤x<−10.60−1≤x<00.900≤x<111≤x<∞
Also find (i) P (X<0 ) and (ii) P(X≥−1).
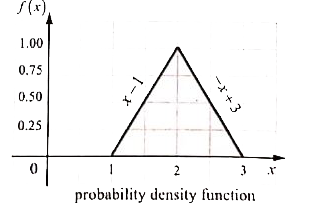
View SolutionIf X is the random variable with porbability density function f(x) given by f(x)=⎧⎪⎨⎪⎩x−11≤x<2−x+32≤x<30otherwise
find (i) the distribution function F(x) (ii) P(1.5≤X≤2.5)
View SolutionIf f(x) = {2x0≤x≤a0otherwise is a probability density function of a random variable then the value of a is ……….. .
View SolutionFor the probability density function f(x) ={2e−2xx>00x≤0 find F(2)
View SolutionThe distribution function F(x) of a random variable X is ……….
View Solution
