If the probability density function of a random variable X is f(x)=π2 in 0≤x≤2, then P(X>1.5X>1) is equal to
A
716
B
34
C
712
D
2164
Text Solution
The correct Answer is:C
|
Similar Questions
Knowledge Check
If the probability density function of a random variable X is f(x)=x2 in 0≤x≤2, then P(X>1.5∣X>1) is equal to
A716B34C712D2164If the probability density function of a continuous random variable X is f(x)={3+2x182≤x≤40x<2 orx>4 Then the mathematical expectation of X is
A8327B2783C8723D3872If the p.d.f of a random variable X is
F(x)={0.5x0≤x≤20otherwise
Then the value of P(0.5≤X≤1.5) isA14B12C34D1
The probability distribution of a random variable X is given below
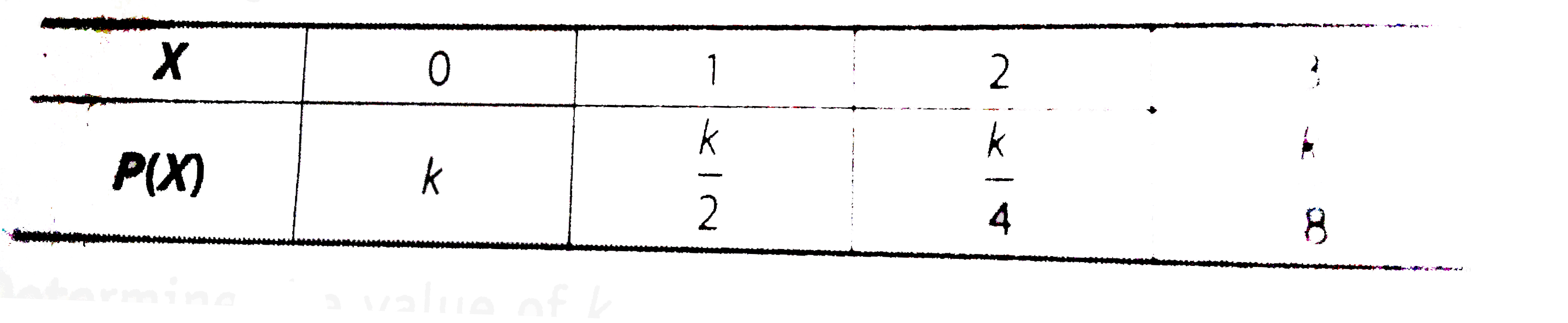
(i) Determine the value of K .
(ii) Determine P(X≤2)andP(X>2).
(iii) Find P(X≤2)+P(X>2).
View SolutionX is continuous random variable with probability density function f(x)=x28,0≤x≤1. Then, the value of P(0.2≤X≤0.5) is
View SolutionIf a random variable waiting time in minutes for bus and probability density function of x is given by
f(x)={15,0≤x≤50,otherwise
Then probability of waiting time not more than 4 minutes is equal to
View SolutionThe p.d.f. of a.c.r. X is
f(x)={12,0<x<20,otherwise
Then P (X<1.5)andP(X>1) are
View SolutionIff(x)={2x2+1x≤14x3−1x>1then ∫20f(x)dx is equal to
View Solution

