The probability density function of X is given by f(x) = {ke−x3for x>00for x≤0
Find (i) the value of k (ii) the distribution function (iii) P(X<3) (iv) P(5≤X) (v) P(X≤4) . Solution in Tamil
Step by step video & image solution for The probability density function of X is given by f(x) = {(ke^(-x/3),"for" " "xgt0),(0, "for" " " xlt=0):} Find (i) the value of k (ii) the distribution function (iii) P(X lt 3) (iv) P(5lt=X) (v) P(X lt=4) . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONSBOOK - FULL MARKSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE -11.4
7 Videos
- PROBABILITY DISTRIBUTIONSBOOK - FULL MARKSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE -11.5
9 Videos
- PROBABILITY DISTRIBUTIONSBOOK - FULL MARKSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE -11.2
7 Videos
- ORDINARY DIFFERENTIAL EQUATIONS BOOK - FULL MARKSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - ADDITIONAL PROBLEMS
40 Videos
- SAMPLE PAPER - 1 BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 1 EXERCISE - PART-IV (Answer the questions)
14 Videos
Similar Questions
Two balls are drawn in succession without replacement from an urn containing four red balls and three black balls. Let X be the possible outcomes drawing red balls. Find the probability mass function and mean for X.
View SolutionCompute P(X=k) for the binomial distribution , B (n,p) where
(i) n=6 , p=13,k=3 (ii) n=10 ,p=15 ,k=4 (iii) n = 9 , p=12 , k =7
View SolutionThree fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
View SolutionFind the order and degree of the following differential equations
(i) dydx+y=x2
(ii) y'+y2=x
(iii) y'+3y2+y3=0
(iv) d2ydx2+x=√y+dydx
(v) d2ydx2−y+dydx+d3y(dx3)32=0
(vi)y'=(y−y'3)2/3
(vii)y'+(y2)=(x+y2)
(viiii)y'+(y)2=x(x+y)2 (ix)dy(dx)2+x=dxdy+x2
(x) sinx(dx+dy)=cosx(dx−dy)
View SolutionBy using Gaussian elimination method, balance the chemical reaction equation:
C2H6+O2→H2O+CO2.
View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निचे दिया गया है |
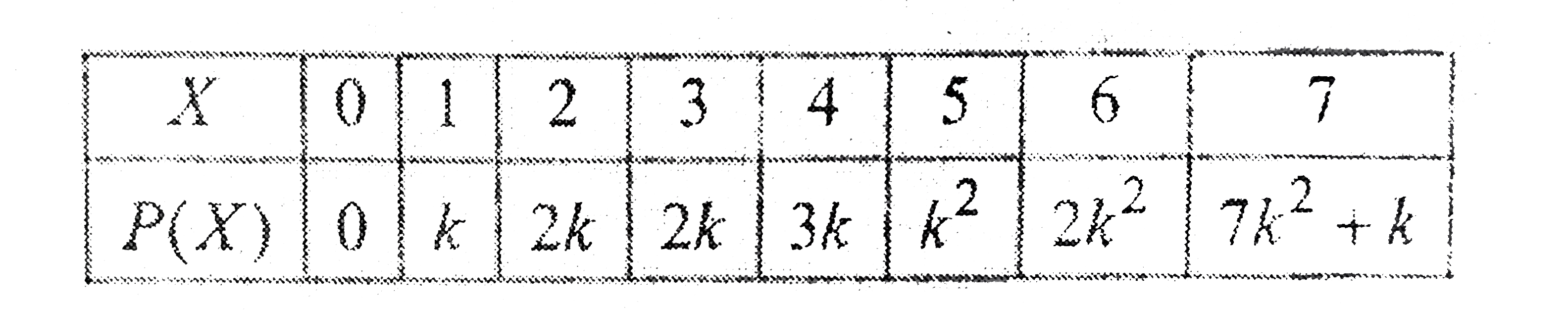
(i) K
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionThe probability density function of X is given by f(x)={ke−x3for x>00for x≤0
Find
P(X<3)
View SolutionThe probability density function of random variable X is given by f(x)={k1≤x<50otherwise
Find (i) Distribution function (ii) P(X<3) (iii)P(2<X<4)(iv)P(3≤X)
View SolutionA random variable X has the following probability distribution :

Determine
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3).
View SolutionA random variable X has a probability density function f(x)={k0<x<2π0elesewhere find (i) k , (ii) P(0<X<π/2) (iii) P(π/2<X<3π/2)
View SolutionA random variable X has the following probability distribution:

Determine
(i) K (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution:

Determine
(i) K (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution:

Determine (i) K (ii) P(X<3) (iii) P(X>6) (iv) P(0<X<3)
View Solutionएक यादृच्छिक चर का प्रायिकता बंटन नीचे दिया गया है

ज्ञात कीजिये
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution:

Determine (i)k,(ii)P(X<3),(iii)P(0<X<3),(iv)P(X>4).
View Solution
