The probability density function of random variable X is given by f(x)={k1≤x<50otherwise
Find (i) Distribution function (ii) P(X<3) (iii)P(2<X<4)(iv)P(3≤X) Solution in Tamil
Step by step video & image solution for The probability density function of random variable X is given by f(x)={(k,1lt=xlt5),(0,"otherwise"):} Find (i) Distribution function (ii) P(X lt 3) " (iii)" P(2ltX lt4) "(iv)" P(3 lt=X) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONSBOOK - FULL MARKSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE -11.1
5 Videos
- PROBABILITY DISTRIBUTIONSBOOK - FULL MARKSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE -11.2
7 Videos
- ORDINARY DIFFERENTIAL EQUATIONS BOOK - FULL MARKSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - ADDITIONAL PROBLEMS
40 Videos
- SAMPLE PAPER - 1 BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 1 EXERCISE - PART-IV (Answer the questions)
14 Videos
Similar Questions
Suppose X is the number of tails occurred when three fair coins are tossed once simultaneously. Find the values of the random variable X and number of points in its inverse images .
View SolutionThree fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
View SolutionFind the order and degree of the following differential equations
(i) dydx+y=x2
(ii) y'+y2=x
(iii) y'+3y2+y3=0
(iv) d2ydx2+x=√y+dydx
(v) d2ydx2−y+dydx+d3y(dx3)32=0
(vi)y'=(y−y'3)2/3
(vii)y'+(y2)=(x+y2)
(viiii)y'+(y)2=x(x+y)2 (ix)dy(dx)2+x=dxdy+x2
(x) sinx(dx+dy)=cosx(dx−dy)
View SolutionBy using Gaussian elimination method, balance the chemical reaction equation:
C2H6+O2→H2O+CO2.
View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निम्नलिखित दिया गया है-

(i) k
(ii) P(X<4)
(iii) P(X<5)
(iv) P(X<6)
View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निचे दिया गया है |
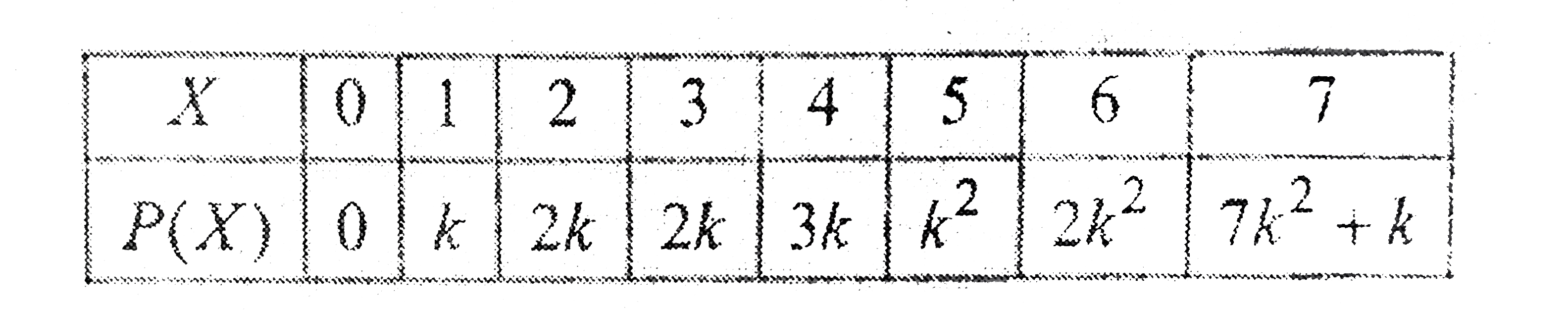
(i) K
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionIf f(x)= kx, 0 lt x lt 2 = 0 otherwise, is a probability density function of a random variable X , then find (i) value of k, (ii) P(1 lt x lt2).
View SolutionIf X is the random variable with probability density function f(x) is given by
f(x)=⎧⎪⎨⎪⎩x+1−1≤x<0−x+10≤x<10otherwise
then find (i) the distribution function F(x) (ii) P(−0.5≤X≤0.5)
View SolutionThe probability density function of X is f(x) = ⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find (i) P(0.2≤X<0.6)(ii)P(1.2≤X<1.8)(iii)P(0.5 lt=X lt 1.5)
View SolutionThe probability density function of X is given by f(x) = {ke−x3for x>00for x≤0
Find (i) the value of k (ii) the distribution function (iii) P(X<3) (iv) P(5≤X) (v) P(X≤4) .
View SolutionThe following is a probability distribution function of a random variable :

(i) Find k (ii) Find P(X>3) (iii) Find P(−3<X<4)
(iv) Find P(X<−3).
View SolutionA random variable X has the following probability distribution :

Determine
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3).
View SolutionA random variable X has the following probability distribution.
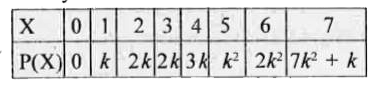
i. k, ii. P(X<3) iii. P(X>6) iv. (P(0<X<3)
View SolutionA random variable X has a probability density function f(x)={k0<x<2π0elesewhere find (i) k , (ii) P(0<X<π/2) (iii) P(π/2<X<3π/2)
View SolutionA random variable X has the following probability distribution:

Determine
(i) K (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3)
View Solution
