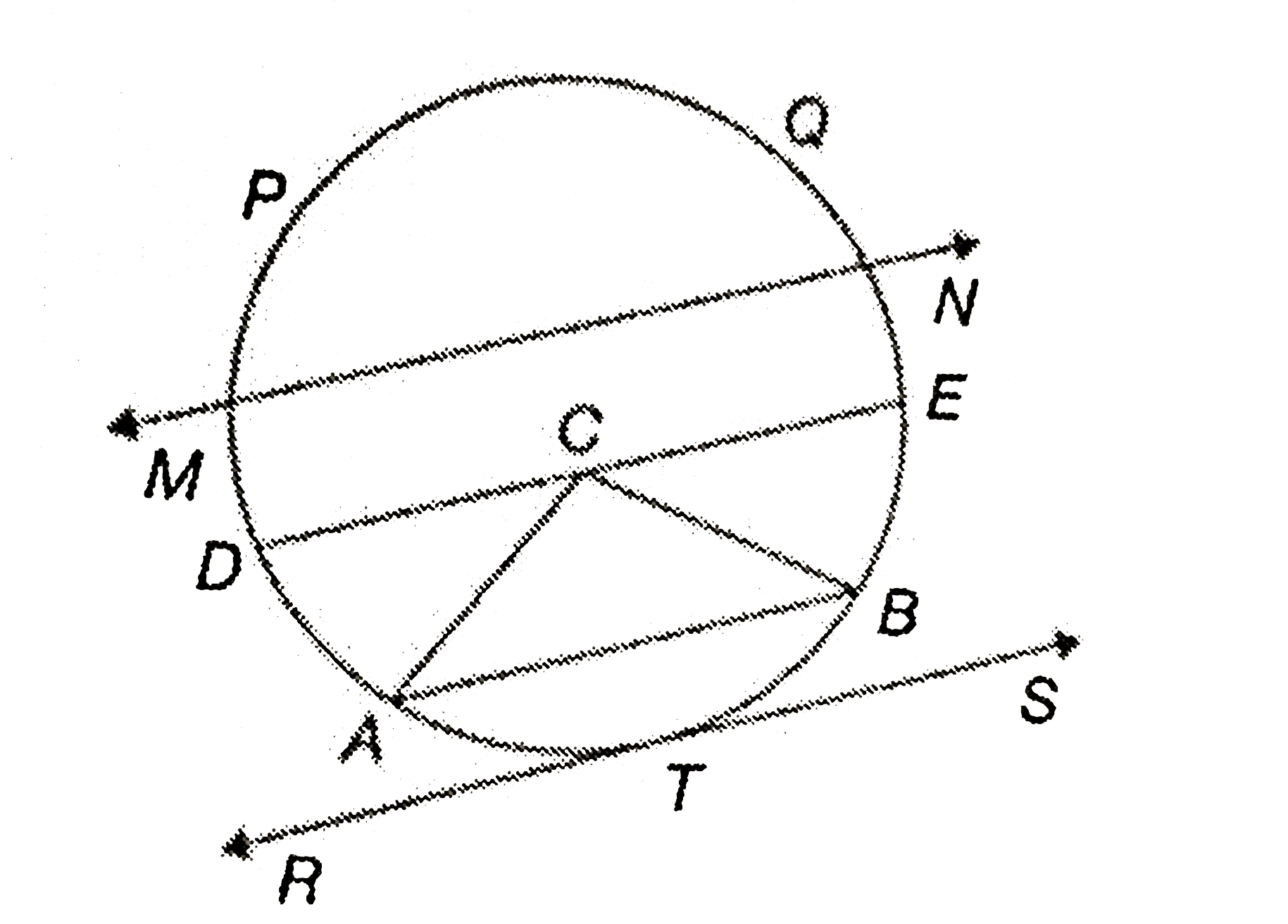
The region bounded by the line segment AB and the part of the circle ATB is called ________ of the circle.
The correct Answer is:segment
Step by step video, text & image solution for The region bounded by the line segment AB and the part of the circle ATB is called ________ of the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS19videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - CONCEPT APPLICATION5videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - CROSSWORD1videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FRACTIONS AND DECIMALS EXERCISE - Crossword1videos
FRACTIONS AND DECIMALS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENUSRATION EXERCISE - Crossword1videos
MENUSRATION
Similar Questions

P, Q are the points on the circle. The part of the circle, PQ is called ________ of the circle.View Solution
The line RS which touches the circle at T is called _______ to the circle.View Solution
The line intersecting the circle at M and N is called _______ of the circle.View SolutionAny part of a circle is called an………..of the circle.
View SolutionDraw a line segment XY as the diameter of a circle .
View SolutionLet C be the mid-point of an arc AB of a circle such that m ˆAB=1830. If the region bounded by the arc ACB and line segment AB is denoted by S, then the centre O of the circle lies in the interior of S (b) in the exterior of S on the segment AB (d) on AB and bisects AB
View Solution
If A, B are the point on the circle. The line segment ¯¯¯¯¯¯AB is called _______ of the circle.View SolutionA line which intersects a circle at two distinct point is called a ______ of the circle.
View SolutionCHORD OF A CIRCLE A line segment joining any two point on a circle is called a chord of the circle.
View SolutionA line which intersects a circle at two distinct point is called a ______ of the circle.
View Solution

