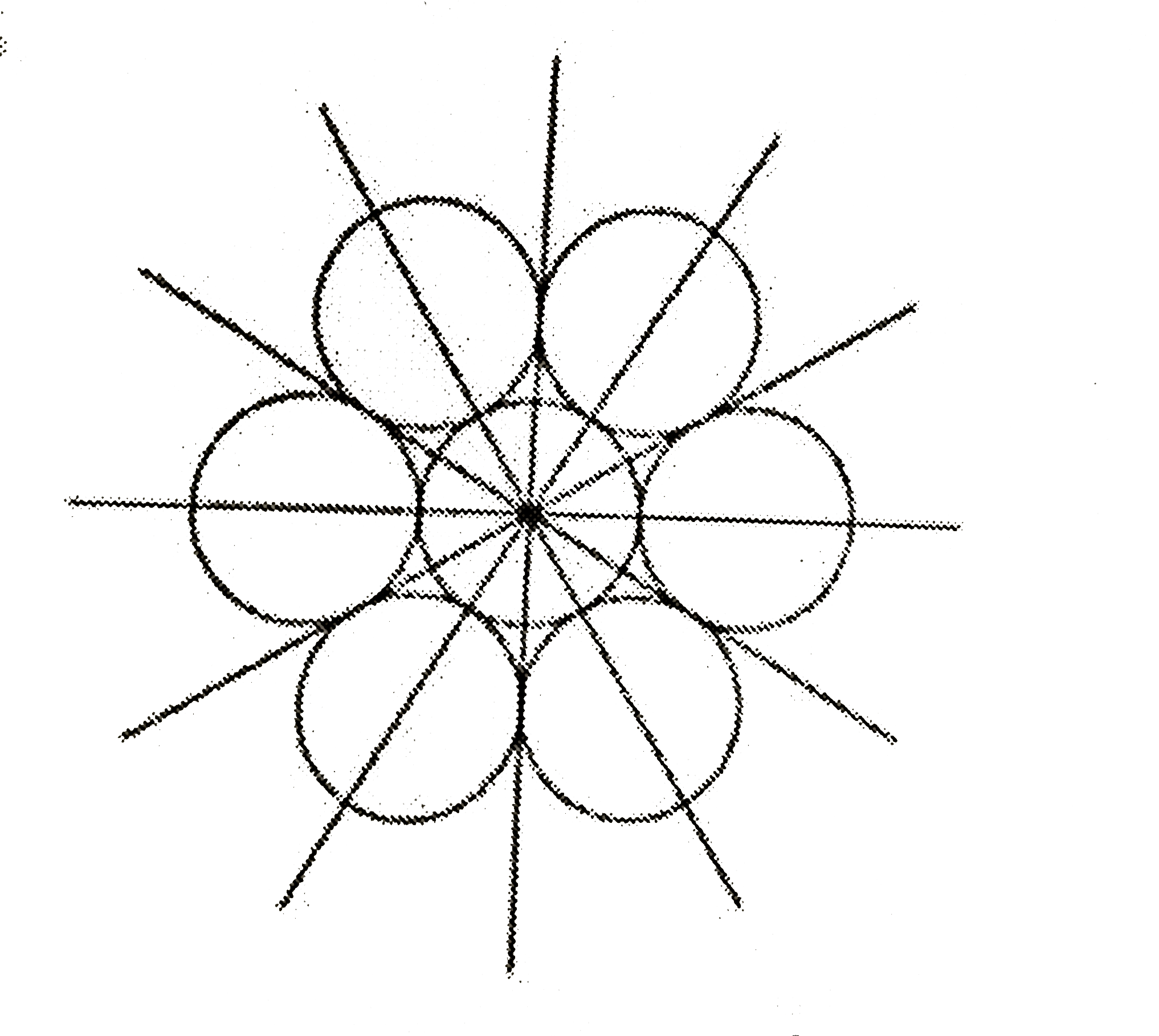
In the given figure, the radii of the circles are equal. The middle circle is touching all the other circles and each of the other circles is touching exactly three circles as shown in the figure. What is the total number of lines of symmetry that can be drawn for the given figure?

A

3

B

6

C

12

D

Infinitely many

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The lines of symmetry are shown in the figure.
The number of lines of symmetry is 6.

Hence, the correct option is (b).

|

Updated on:21/07/2023

Class 6 MATHS PRACTICAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The two circles touch each other if
A $c = \sqrt{a^{2} + b^{2}}$
B $\frac{1}{c} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$
C $c = \frac{1}{a^{2}} + \frac{1}{b^{2}}$
D $c = \frac{1}{a^{2} + b^{2}}$
Question 2 - Select One
The number of circles that can be drawn touching both the given circles is

A2
B3
C4
D5
Question 3 - Select One
Three equal circles of unit radius touch each other. Then, the area of the circles is
A $\frac{π}{3} {(2 + \sqrt{3})}^{3}$
B $\frac{2 π}{3} (2 + \sqrt{3 P P^{2}})$
C $6 π {(2 + \sqrt{3})}^{2}$
D $\frac{1}{6} π {(2 + \sqrt{3})}^{2}$

PEARSON IIT JEE FOUNDATION-GEOMETRY-CONCEPT APPLICATION

Home
Ask Doubt
Profile