बायो-सावर्ट नियम को सूत्र सदिश रूप में लिखिए| किसी धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र का व्यंजक प्राप्त कीजिये| आवश्यक चित्र बनाइये|

Text Solution

Verified by Experts

बायो-सावर्ट नियम - इसके अनुसार किसी धारावाही तार के अल्पांश लम्बाई के कारण किसी बिंदु पर उत्पन्न चुंबकीय क्षेत्र-
(i) चालक में प्रवाहित धारा 1 के अनुक्रमानुपाती होता है|
$δ B \propto l$
(ii) यह चालक के उस अल्पांश की लम्बाई $(\vec{δ} l)$ के अनुक्रमानुपाती होता है|
$δ B \propto \sin θ$
(iv) यह अल्पांश से बिंदु P की दुरी के वर्ग के व्युत्क्रमानुपाती होता है|
$∴ δ \vec{B} \propto \frac{i | δ l | \sin θ}{r^{2}}$

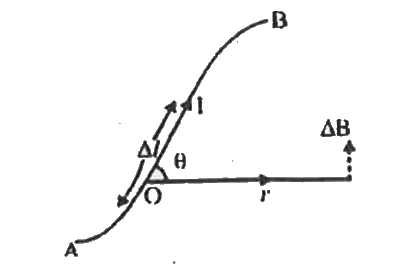
अतएव $| δ \vec{B} | \propto \frac{μ_{0}}{4 π} \frac{i | \vec{δ} l | \sin θ}{r^{2}}$
यदि चालक निर्वात (अथवा वायु) में रखा तो, तो चुंबकीय क्षेत्र
$μ_{0}$ का मान $4 π \times 10^{- 7}$ न्यून्टन/ $ए म ् प ि य र^{2}$ होता है|
सदिश संकेतों के रूप में-
$δ \vec{B} = \frac{μ_{0} i \vec{δ} l \times \vec{r}}{4 π l r^{3}}$
वृत्ताकर कुंडली के अक्ष पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र- निम्न चित्र में a त्रिज्या की एक वृत्ताकार कुंडली है जो yz तल में स्तिथ है| इसमें I एम्पियर की धारा प्रवाहित हो रही है| इस कुंडली का अक्ष X दिशा की और है जिस पर x मि. दुरी पर स्तिथ किसी बिंदु P पर चुंबकीय क्षेत्र ज्ञात करना है|

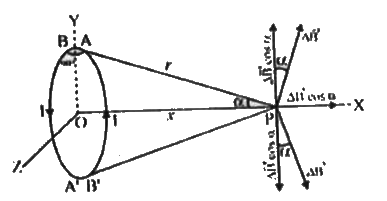
कुंडली को छोटे-छोटे अल्पाँशों में बांटा गया है| माना AB की लम्बाई $Δ l$ है, इस अल्पांश से P की दुरी r है| P पर चुंबकीय क्षेत्र-
$Δ \vec{B} = \frac{μ_{0}}{4 π} \frac{l Δ l \times \vec{r}}{r^{3}}$ ........(1)
$Δ B = \frac{μ_{0}}{4 π} \frac{l Δ l \sin θ}{r^{2}}$ ........(2)
$θ = 90^{\circ}$ होने पर
$Δ B = \frac{μ_{0}}{4 π} \frac{l Δ l {\sin 90}^{\circ}}{r^{2}}$
$Δ B = \frac{μ_{0}}{4 π} = \frac{I Δ l}{r^{2}}$ ..........(3)
AB के कारण अक्ष के लंबरूप क्षेत्र का घातक परस्पर बराबर एवं विपरीत होने के कारन एक-दूसरे को निरस्त कर देते है, परन्तु दोनों के अक्षीय घातक एक ही दिशा में होने के कारन जुड़ जाते है| इसी तरह कुंडली की पूरी परिधि को व्यासतः अभिमुख अल्पाँशी में विभाजित करके समझ सकते है|
बिंदु P पर परिणामी चुंबकीय क्षेत्र, उसकी अक्ष के अनुदिश घटकों के योग के तुल्य होगा| अर्थात
$B = \sum A B \sin α$
चित्र से $\sin α = I \frac{a}{r}$
$∴ B = \sum \frac{μ_{0}}{4 π} (I Δ \frac{I}{r^{2}} \times \frac{a}{r})$
$= \frac{μ_{0}}{4 π} \frac{I a}{r^{3}} \sum Δ l$
$Δ l = 2 π a$
$∴ B = \frac{μ_{0}}{4 π} \frac{I a}{r^{3}} \times 2 π a$
$B = \frac{μ_{0}}{4 π} \times \frac{2 π a^{2} I}{r^{3}}$ ..........(4)
यदि कुंडली में n फेरे है|
$∴ B = \frac{μ_{0}}{4 π} \times \frac{2 π a^{2} n l}{r^{3}}$ वेबर/ $म ी^{2}$
चित्र से, $r = {(a^{2} + x^{2})}^{\frac{1}{2}}$
$∴ r^{3} = {(a^{2} + x^{2})}^{\frac{3}{2}}$
$∴ B = \frac{μ_{0}}{4 π} \times \frac{2 π a^{2} n l}{{(a^{2} + x^{2})}^{\frac{3}{2}}}$ ........(5)
धारावाही कुंडली के अक्ष के किसी बिंदु पर चुंबकीय क्षेत्र समीकरण (4) या (5) से प्राप्त होता है एवं इस क्षेत्र की दिशा अक्ष के अनुदिश होती है|

Updated on:21/07/2023

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

TRIPUTI PUBLICATION-विघुत धारा के चुंबकीय प्रभाव -निबंधात्मक प्रशन

Home
Ask Doubt
Profile