एक लम्बे ठोस बेलनाकार धारावाही चालक के कारण उसके (i) बाहर तथा (ii) अंदर स्थित बिंदु पर चुंबकीय क्षेत्र का व्यंजक प्राप्त कीजिए| आवश्यक चित्र बनाइये|
(i) बेलन के बाहर चुंबकीय क्षेत्र का मान- चित्र में एक R त्रिज्या का ठोस धारावाही बेलन दर्शाया गया है, जिसमे 1 मान की धारा प्रवाहित हो रही है| बेलन के अक्ष से r दुरी पर एक बिंदु P पर स्तिथ है, जहाँ चुंबकीय क्षेत्र का मान ज्ञात करना है|
इसके लिए हम r त्रिज्या के वृत्ताकार पथ की कल्पना करते है| साथ ही P बिंदु पर एक dl लम्बाई के अल्पांश की भी कल्पना करते है| अल्पांश →dl चुंबकीय क्षेत्र →B समान दिशा में है|
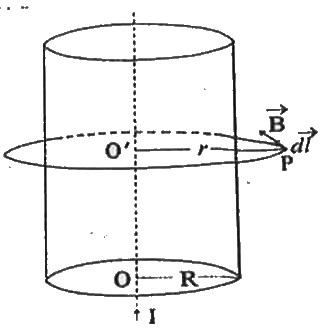
एम्पियर के नियम से-
∮→B.→dl=μ0∑I
∮Bdl=μ0I
B∮dl=μ0I[∮dl=परिधी=2πr]
B×2πr=μ0l
B=μ0I2πr.......(1)
चुंबकीय क्षेत्र B,धारा I के समानुपाती है,
B∝I
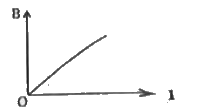
चुंबकीय क्षेत्र का मान r के व्युत्क्रमानुपाती होता है|
B∝I/r
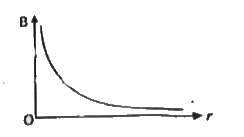
(ii) बेलन की सतह पर चुंबकीय क्षेत्र का मान समी. (1) में r=R रखने पर
B=μ0I2πR.......(2)
(iii) बेलन की सतह के अंदर चुंबकीय क्षेत्र का मान- अब हमें बेलन के अंदर, बेलन के अक्ष से r दुरी पर चुंबकीय क्षेत्र का मान ज्ञात करना है| इसके लिए बेलन के अंदर r त्रिज्या के वृत्ताकार पथ पर एक →dl लम्बाई के अल्पांश की भी कल्पना करते है| एम्पियर के नियम से
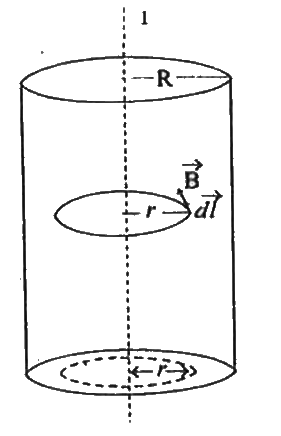
∮→B.→dl=μ0∑I
∮→Bcosθ=μ0∑I
B×2πr=μ0I.
B=μ0I.2πr
I. - की गड़ना - ∴πR2 अनुपस्थ काट से प्रवेशित धारा =1
∴ अनुप्रस्थ काट में प्रदर्शित धारा =1πR2
πr2 अनुपृष्ठ काट में प्रदर्शित धारा
I.=1πR2×πr2
I.=Ir2R2⇒B=μ02πr×Ir2R2
B=μ0Ir2πR2
समी. (3) से B∝r
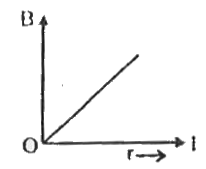
अर्थात बेलन के अंदर, अक्ष से दुरी बढ़ने पर चुंबकीय क्षेत्र का मान भी बढ़ता है|
समी.(1), (2) & (3) से चुंबकीय क्षेत्र B के, (r) के साथ परिवर्तन को बताने वाला संयुक्त ग्राफ निम्न है-
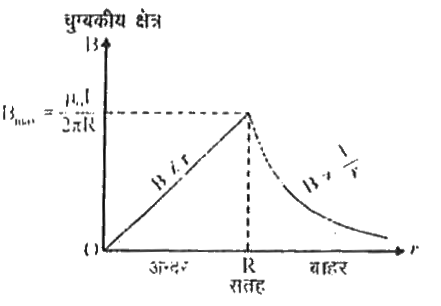
सबसे अधिकतम चुंबकीय क्षेत्र का मान बेलन की सतह पर होता है|
Topper's Solved these Questions
- विघुत धारा के चुंबकीय प्रभाव BOOK - TRIPUTI PUBLICATIONCHAPTER - विघुत धारा के चुंबकीय प्रभाव EXERCISE - आंकिक प्रशन
2 Videos
- विघुत धारा के चुंबकीय प्रभाव BOOK - TRIPUTI PUBLICATIONCHAPTER - विघुत धारा के चुंबकीय प्रभाव EXERCISE - लघुत्तरात्मक प्रशन
2 Videos
- प्रकाश विधुत प्रभाव एवं द्रव्य तरंगे BOOK - TRIPUTI PUBLICATIONCHAPTER - प्रकाश विधुत प्रभाव एवं द्रव्य तरंगे EXERCISE - एकांकी प्रश्न
8 Videos
- विद्युत चुम्बकीय तरंगें, संचार एवं समकालीन भौतिकी BOOK - TRIPUTI PUBLICATIONCHAPTER - विद्युत चुम्बकीय तरंगें, संचार एवं समकालीन भौतिकी EXERCISE - आंकिक प्रश्न
3 Videos
Similar Questions
0.5 मीटर त्रिज्या के साइक्लोट्रोन में 1.5 टेस्ला का चुंबकीय क्षेत्र लगाया गया है| इसमें गतिशील प्रोटोन के त्वरण के लिए प्रत्यावर्ती विभव की आवृति क्या होगी? प्रोटोन की अधिकतम ऊर्जा का मान भी ज्ञात कीजिए|
View Solutionसाइक्लोट्रोन के सिद्धांत का कथन दीजिए| इस मशीन के कोई दी उपयोग लिखिए|
View Solutionसीजियम धातु के लिए देहली आवृत्ति 5.16×10−14Hz है । इसका कार्य फलन eV में ज्ञात कीजिए ।
View Solutionदिक् काल (मुक्त आकाश) में किसी बिन्दु पर विद्युत क्षेत्र सदिश (→E) का परिमाण 9.3 V/m है। इस बिन्दु पर चुम्बकीय क्षेत्र सदिश (→B) का परिमाण ज्ञात कीजिए।
View Solutionचुंबकीय क्षेत्र में किसी विद्युत धारावाही चालक पर बल
View Solutionकिसी विद्युत धारावाही चालक के कारण चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
View Solutionविद्युत् धारावाही पाश के कारण चुंबकीय क्षेत्र
View SolutionJEE Special |धारावाही चालक के कारण चुंबकीय क्षेत्र | Part 1
View SolutionJEE Special |धारावाही चालक के कारण चुंबकीय क्षेत्र | Part 2
View Solutionकिसी विद्युत् धारावाही चालक के कारण चुम्बकीय क्षेत्र
View Solutionधारावाही वलय , पट्टिका के कारण चुंबकीय क्षेत्र
View Solutionधारावाही वलय के अक्ष पर चुंबकीय क्षेत्र
View Solutionअनन्त लम्बाई के ठोस बेलनाकार चालक का चुंबकीय क्षेत्र
View Solutionचुंबकीय क्षेत्र में धारावाही चालक तार पर बल
View Solutionधारावाही चालक तार के कारण चुम्बकीय क्षेत्र
View Solution
