the median AB of ΔABC is bisected at Eand BE is produced to meet the side AC in f.then the ratio AF:FC=
A
3/4
B
1/3
C
1/2
D
1/4
Video Solution
Text Solution
Let position vector of A w.r.t. B is a and that of C w.r.t. B is c.

Position vector fo D w.r.t.
B=0+c2=c2
Position vector of
E=a+c22=a2+c4 . . . (i)
Let AF:FC=λ:1andBE:EF=μ:1
Position vector of F=λc+a1+λ
Now, position vector of
E=μ(λc+a1+λ)+1⋅0μ+1 . . . (ii)
From eqs. (i) and (ii), we get
a2+c4=μ(1+λ)(1+μ)a+λu(1+λ)(1+μ)c
⇒12=μ(1+λ)(1+μ)
and 14=λμ(1+λ)(1+μ)
⇒λ=12
∴AFAC=AFAF+FC=λ1+λ=1232=13.
|
Similar Questions
Knowledge Check
The median AD of a triangle ABC is bisected at F, and BF is produced to meet the side AC in P. If AP =λAC, then what is the value of λ.?
A14B12C23D13E is a mid-point of median AD of ΔABC. BE is extended to meet AC at F. In what ratio AC is divided by F.
A2:3B2:1C1:3D3:2The median AD of the triangle ABC is bisected at E and BE meets AC at F. Find AF:FC.
A3/4B1/3C1/2D1/4
The median AD of the triangle ABC is bisected at E and BE meets AC at F. Find AF:FC.
View SolutionThe median AD of the triangle ABC is bisected at E and BE meets AC at F. Find AF:FC.
View SolutionIn ΔABC,D is the mid-pointpoint of BC and E is mid-point of AD.BE is produced to meet the side AC in F.Then BF is equal to
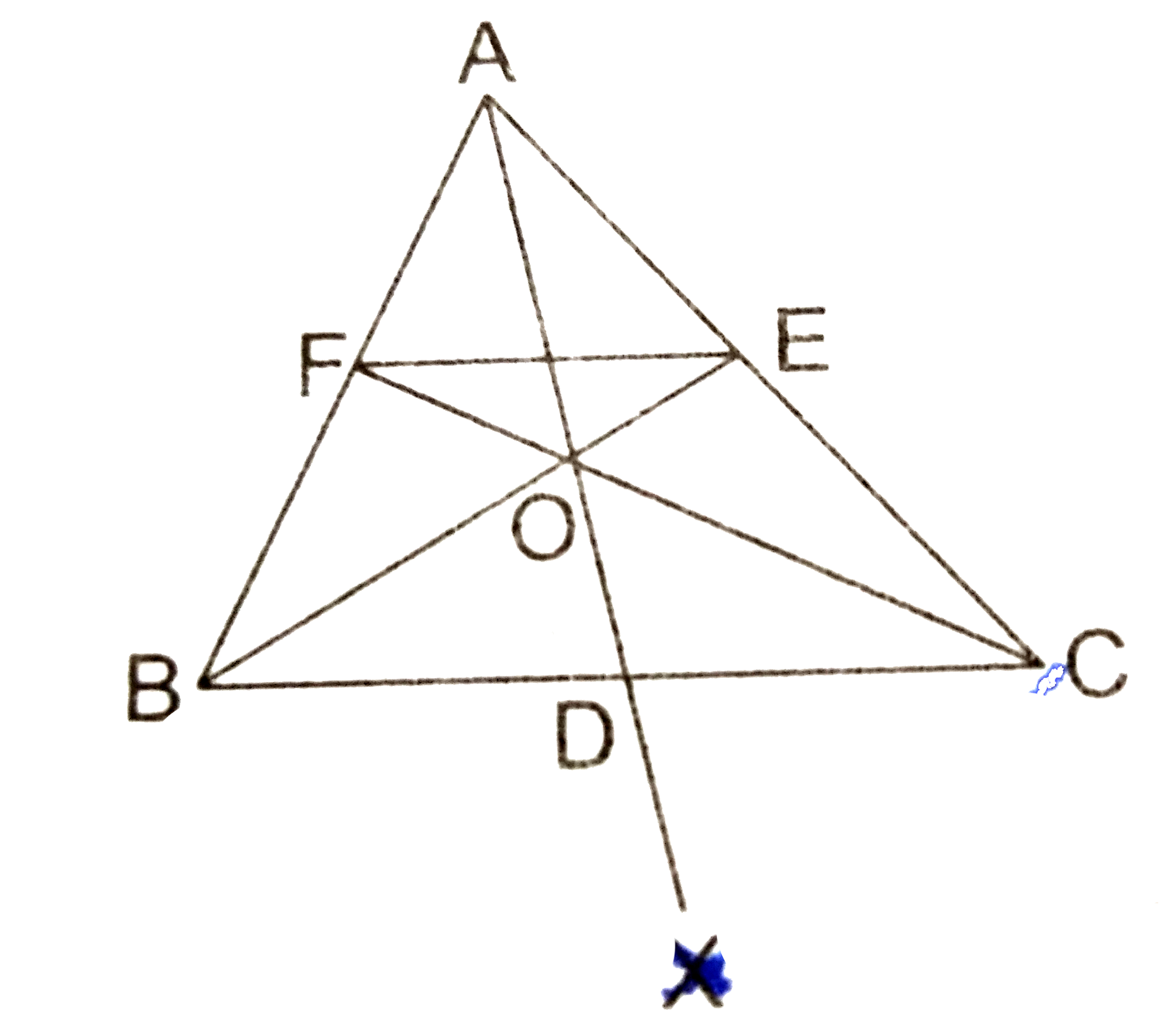
View SolutionIn the given figure, side BC of ΔABC is bisected at D and O is any point AD.BO and CO produced meet AC and AB at E and F respectively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that AO:AX=AF:AB and show that EF∣∣BC.
View SolutionE is the mid-point of the median AD of ΔABC. Line segment BE meets AC at point F when produce, prove that AF=13AC.
View Solution
