Question

In the given figure, side BC of $\Delta ABC$ is bisected at D and O is any point AD.BO and CO produced meet AC and AB at E and F respectively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that $AO:AX=AF:AB$ and show that $EF\mid \mid BC$.

Explanation

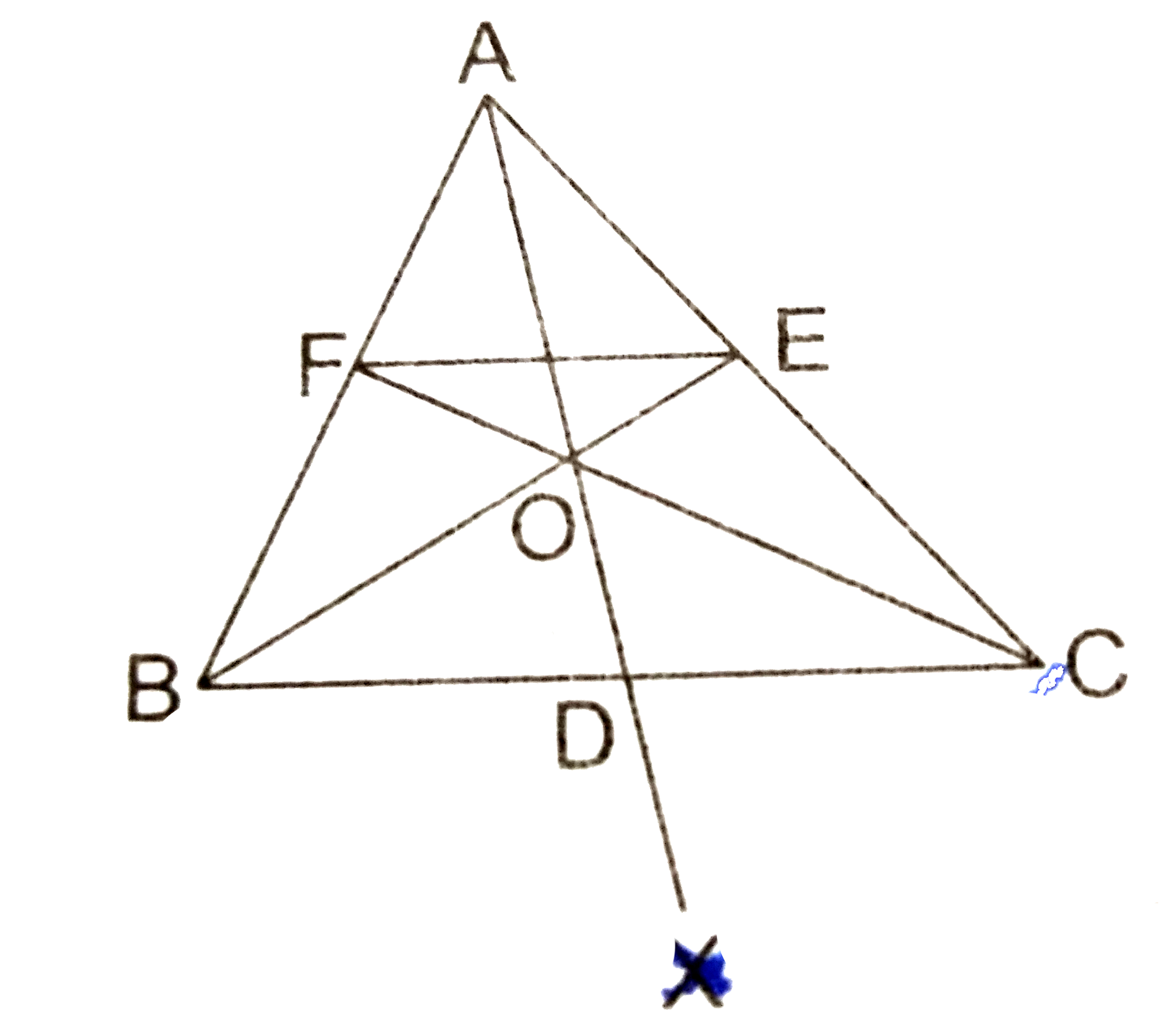
Join BX and CX.
Clearly, `BD=DC and OD =Dx` (given)
Thus,the diagonals of quad. OBXC bisect each other.
`:. OBXC` is a parallelogram.
`:. BX||CF and so, OF||BX`.
Similarly, `OE||XC`.
In `Delta ABX , OF||BX`.
`:. (AO)/(AX)=(AF)/(AB)" "...(i)`
In `Delta ACX, OE||XC`.
`:. (AO)/(AX)=(AE)/(AC)" "...(ii)`
From (i) and (ii) we get `(AF)/(AB)=(AE)/(AC)`
Hence, `FE||BC`.