If a bar of givenlength moves with its extremities on two fixed straight lines at right angles,then the locus of any point on bar marked on the bar describes a/an :
circle
parabola
ellipse
hyerbola
To solve the problem, we will analyze the motion of a bar of fixed length that moves with its extremities on two fixed straight lines that are perpendicular to each other. We will derive the locus of a point on the bar.
1. Set Up the Coordinate System:
- Consider two fixed straight lines that intersect at right angles. We can represent these lines as the x-axis and y-axis in a Cartesian coordinate system.
2. Define the Bar:
- Let the length of the bar be L. The extremities of the bar will touch the x-axis and y-axis. We can denote the endpoints of the bar as points A and B.
3. Position of the Bar:
- Let point A be at (x1,0) on the x-axis and point B be at (0,y1) on the y-axis. The length of the bar can be expressed using the distance formula:
L=√x21+y21
4. Locus of a Point on the Bar:
- Let P be a point on the bar that divides it into two segments in the ratio a:b. The coordinates of point P can be expressed in terms of x1 and y1:
P=(b⋅x1a+b,a⋅y1a+b)
5. Expressing x1 and y1:
- From the length condition, we have:
x21+y21=L2
- Substitute x1 and y1 in terms of P:
x1=a+bbxandy1=a+bay
6. Substituting into the Length Equation:
- Substitute these expressions into the length equation:
(a+bbx)2+(a+bay)2=L2
- Simplifying this gives:
(a+b)2b2x2+(a+b)2a2y2=L2
7. Final Form:
- Dividing through by L2 leads to:
x2(bLa+b)2+y2(aLa+b)2=1
- This is the standard form of the equation of an ellipse.
Conclusion:
The locus of any point on the bar, as it moves with its extremities on two fixed straight lines at right angles, describes an ellipse.
- Consider two fixed straight lines that intersect at right angles. We can represent these lines as the x-axis and y-axis in a Cartesian coordinate system.
- Let the length of the bar be L. The extremities of the bar will touch the x-axis and y-axis. We can denote the endpoints of the bar as points A and B.
- Let point A be at (x1,0) on the x-axis and point B be at (0,y1) on the y-axis. The length of the bar can be expressed using the distance formula:
L=√x21+y21
- Let P be a point on the bar that divides it into two segments in the ratio a:b. The coordinates of point P can be expressed in terms of x1 and y1:
P=(b⋅x1a+b,a⋅y1a+b)
- From the length condition, we have:
x21+y21=L2
- Substitute x1 and y1 in terms of P:
x1=a+bbxandy1=a+bay
- Substitute these expressions into the length equation:
(a+bbx)2+(a+bay)2=L2
- Simplifying this gives:
(a+b)2b2x2+(a+b)2a2y2=L2
- Dividing through by L2 leads to:
x2(bLa+b)2+y2(aLa+b)2=1
- This is the standard form of the equation of an ellipse.
The locus of any point on the bar, as it moves with its extremities on two fixed straight lines at right angles, describes an ellipse.
Topper's Solved these Questions
Similar Questions
A bar of given length moves with its extremities on two fixed straight lines at right angles. Show that any point on the bar describes an ellipse.
View SolutionA bar of length 20 units moves with its ends on two fixed straight lines at right angles. A point P marked on the bar ata distance of 8 units from one end describes a conic whose eccentricity is
View Solution
Knowledge Check
A bar of given length moves with its extremities on two fixed straight lines at right angles. Show that any point on the bar describes an ellipse.
Aa circleBa parabolaCan ellipseDnoneIf the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
Aa parabolaBan ellipseCa hyperbolaDNone of theseA and B are two fixed points. The locus of a point P such that ∠APB is a right angle, is:
 Ax2+y2=a2Bx2−y2=a2C2x2+y2=a2DNone of these
Ax2+y2=a2Bx2−y2=a2C2x2+y2=a2DNone of these
The locus of a point which moves difference of its distance from two fixed straight which are at right angles is equal to the distance from another fixed straight line is
View SolutionIf AOBandCOD are two straight lines which bisect one another at right angles, show that the locus of a points P which moves so that PAxPB=PCxPD is a hyperbola. Find its eccentricity.
View SolutionIf A and B are two fixed points, then the locus of a point which moves in such a way that the angle APB is a right angle is
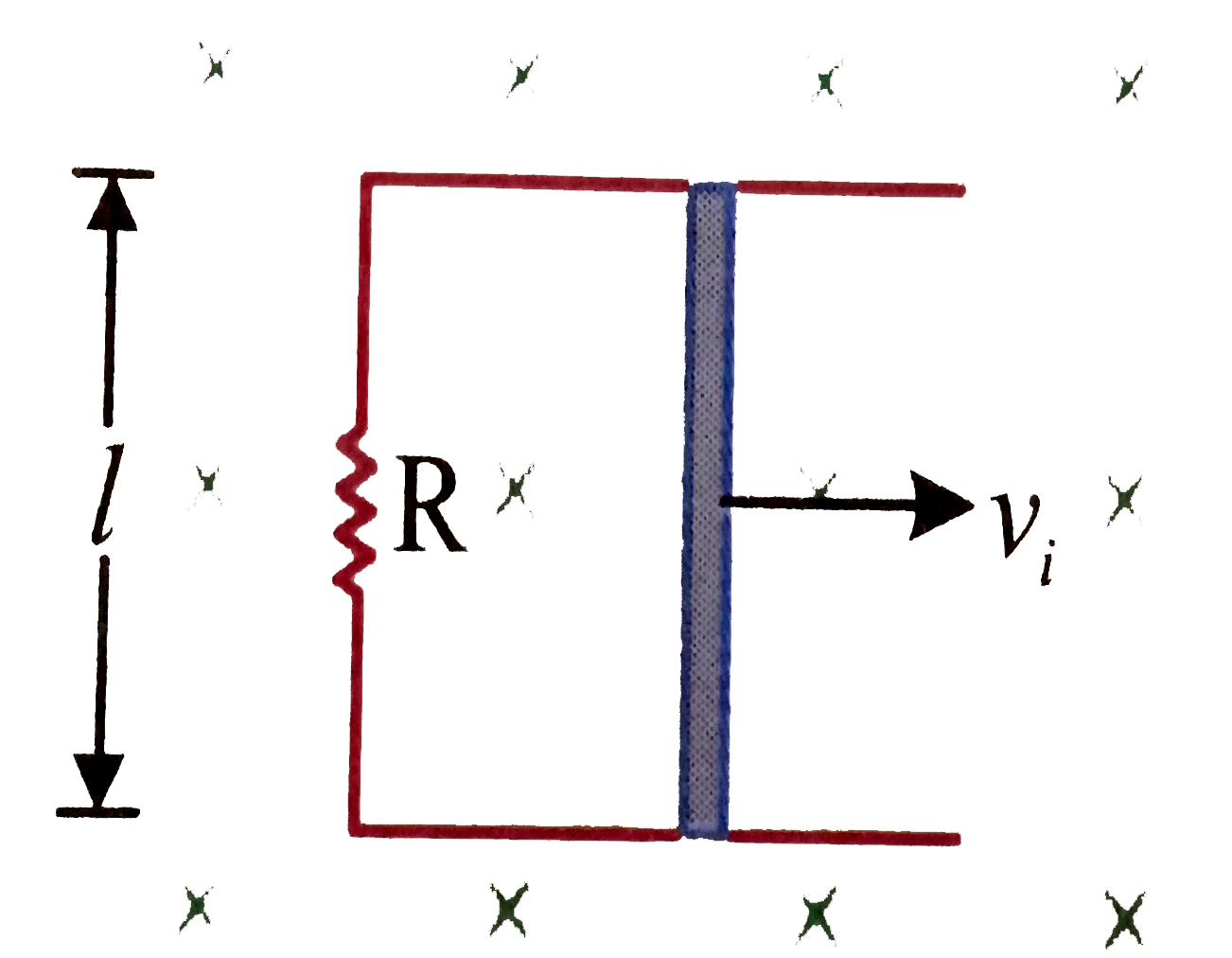
View SolutionA bar of mass m and length l moves on two frictionless parallel rails in the presence of a uniform magnetic field directed into the plane of the paper. The bar is given and initial velocity vi to the right and released. Find the velocity of bar, induced emf across the bar and the current in the circuit as a function of time
View SolutionLet z=x+iy then locus of moving point P(z) 1+¯zz∈R, is
View Solution
