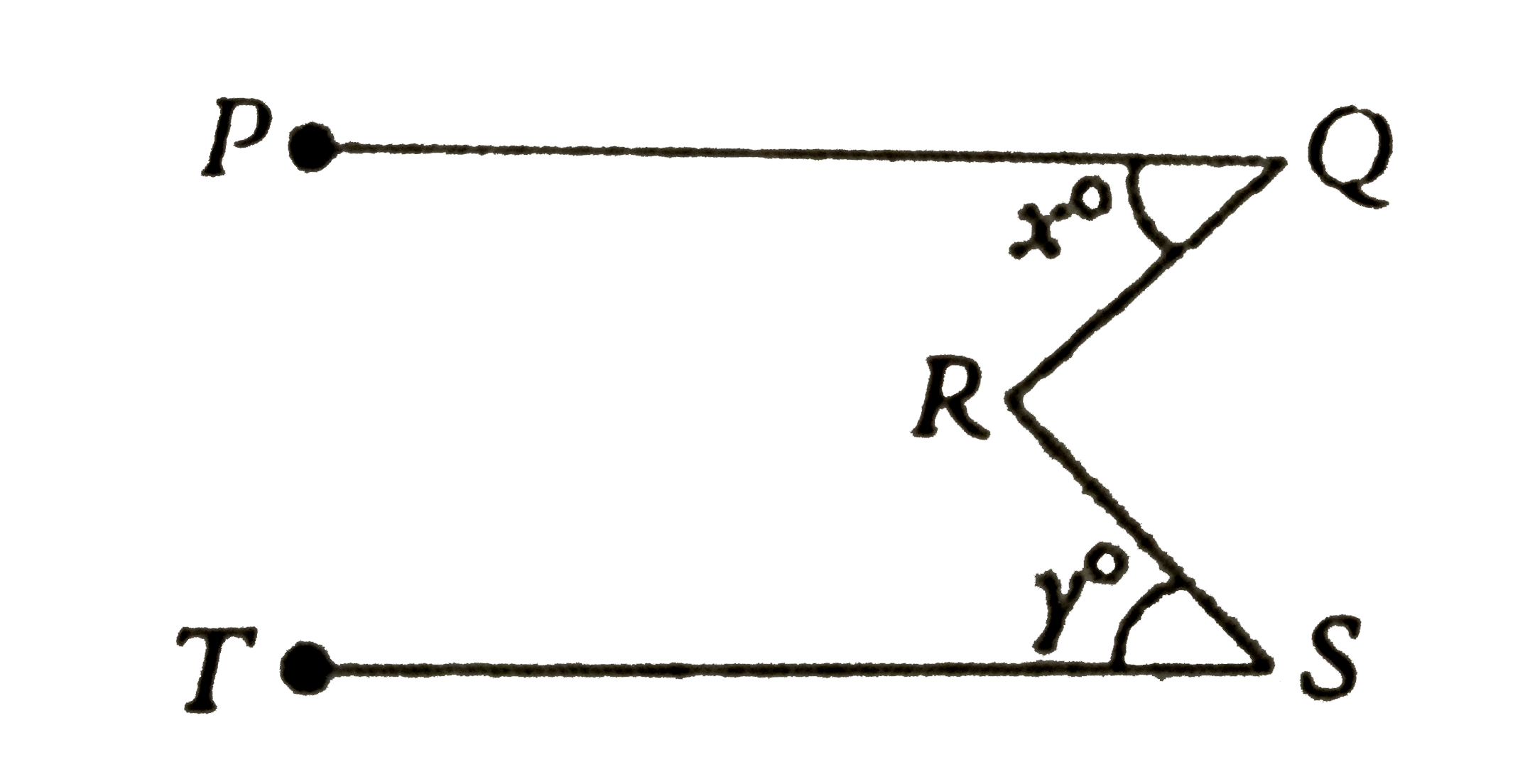
In the given figure (not to scale), ¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯QP∣∣∣∣¯¯¯¯¯¯SD∣∣ and also ¯¯¯¯¯¯QR∣∣¯¯¯¯¯¯DP. Find x
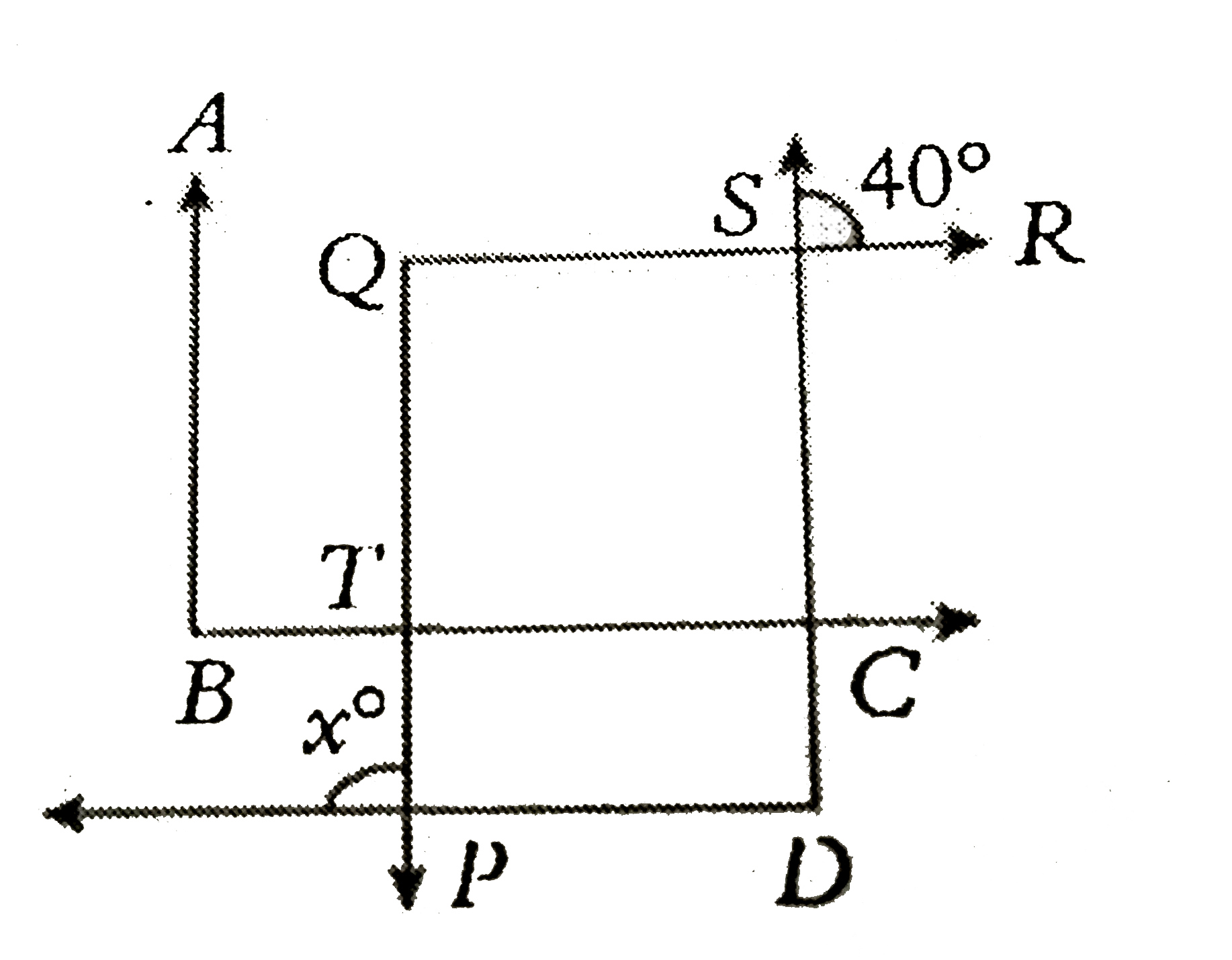
(a) QSDP is a parallelogram.
(b) Find ∠QSC, as vertically opposite angles are equal.
(c ) ∠QSD and ∠SDP are supplementary as they are the angles on the same side of the transversal. Use this to find ∠SDP.
(d) ∠SDP and x are corresponding angles.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very short answer type question25videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short Answer Type Questions 319videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 37videos
Formulae
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)7videos
INDICES
Similar Questions
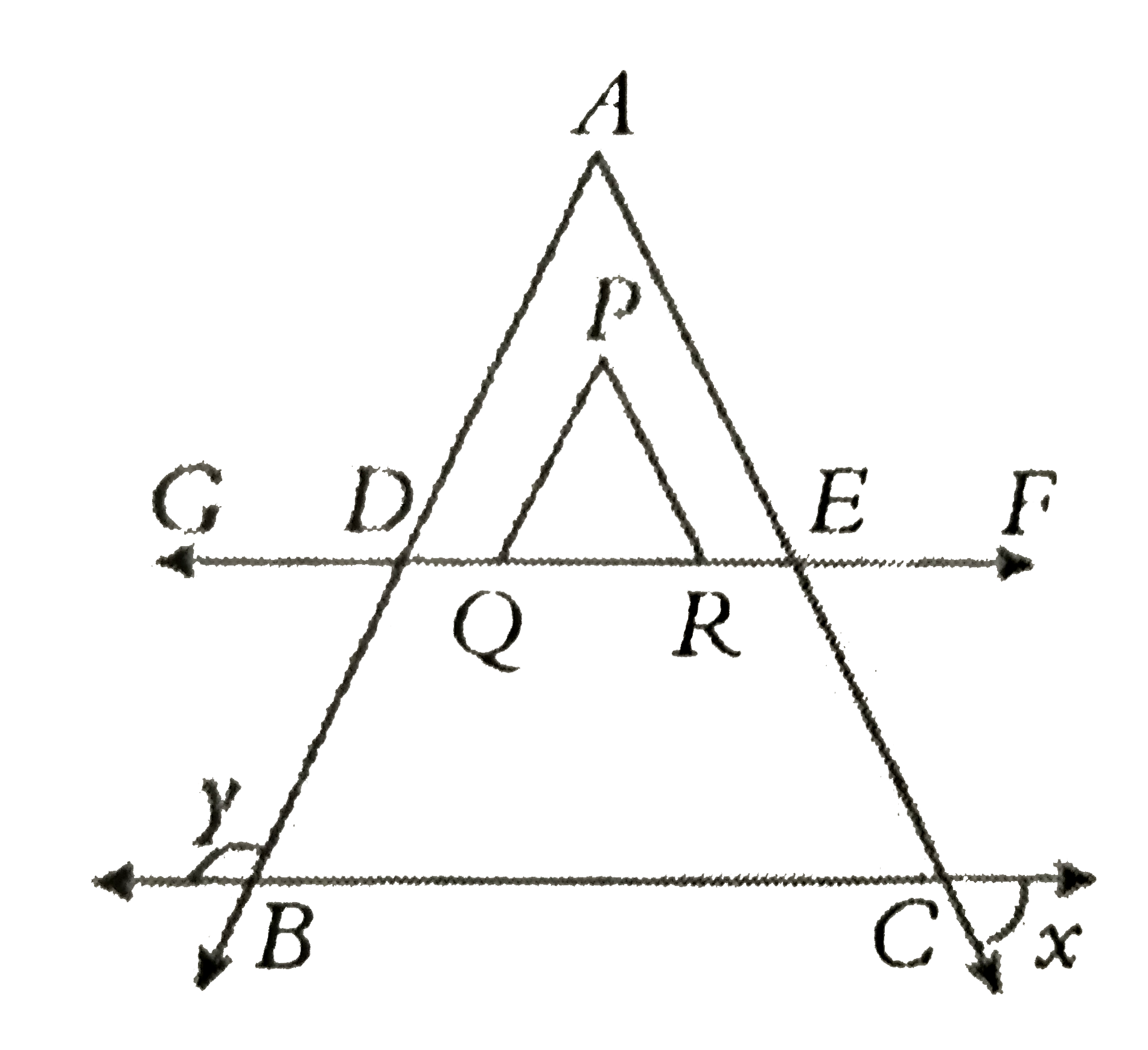
In the above figure (not to scale ), ¯¯¯¯¯¯GF∣∣∣∣¯¯¯¯¯¯BD,¯¯¯B∣∣∣∣¯¯¯¯¯¯PQ and ¯¯¯¯¯¯AC∣∣¯¯¯¯¯¯PR If ∠x=40∘ and ∠y=110∘, then find ∠QPR.View Solution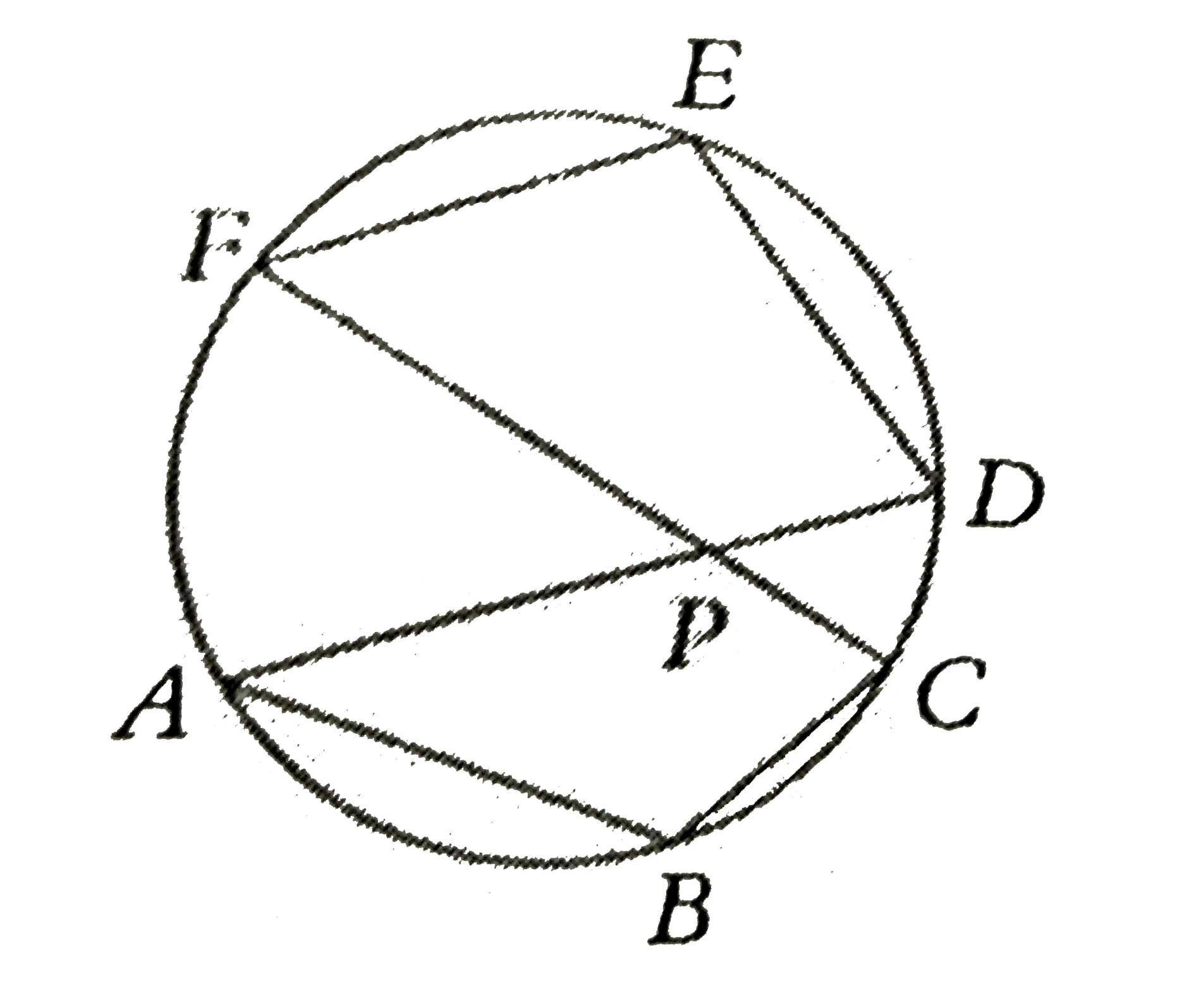
In the above figure (not to scale) ¯¯¯¯¯¯AB,¯¯¯¯¯¯BC,¯¯¯¯¯¯CF,¯¯¯¯¯¯DE and ¯¯¯¯¯¯FE are chords of the circle. If ∠ABC=100∘ and ∠FED=110∘, then ∠FPA= View SolutionFind m∠C in the given figure if ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯DC.
View Solution
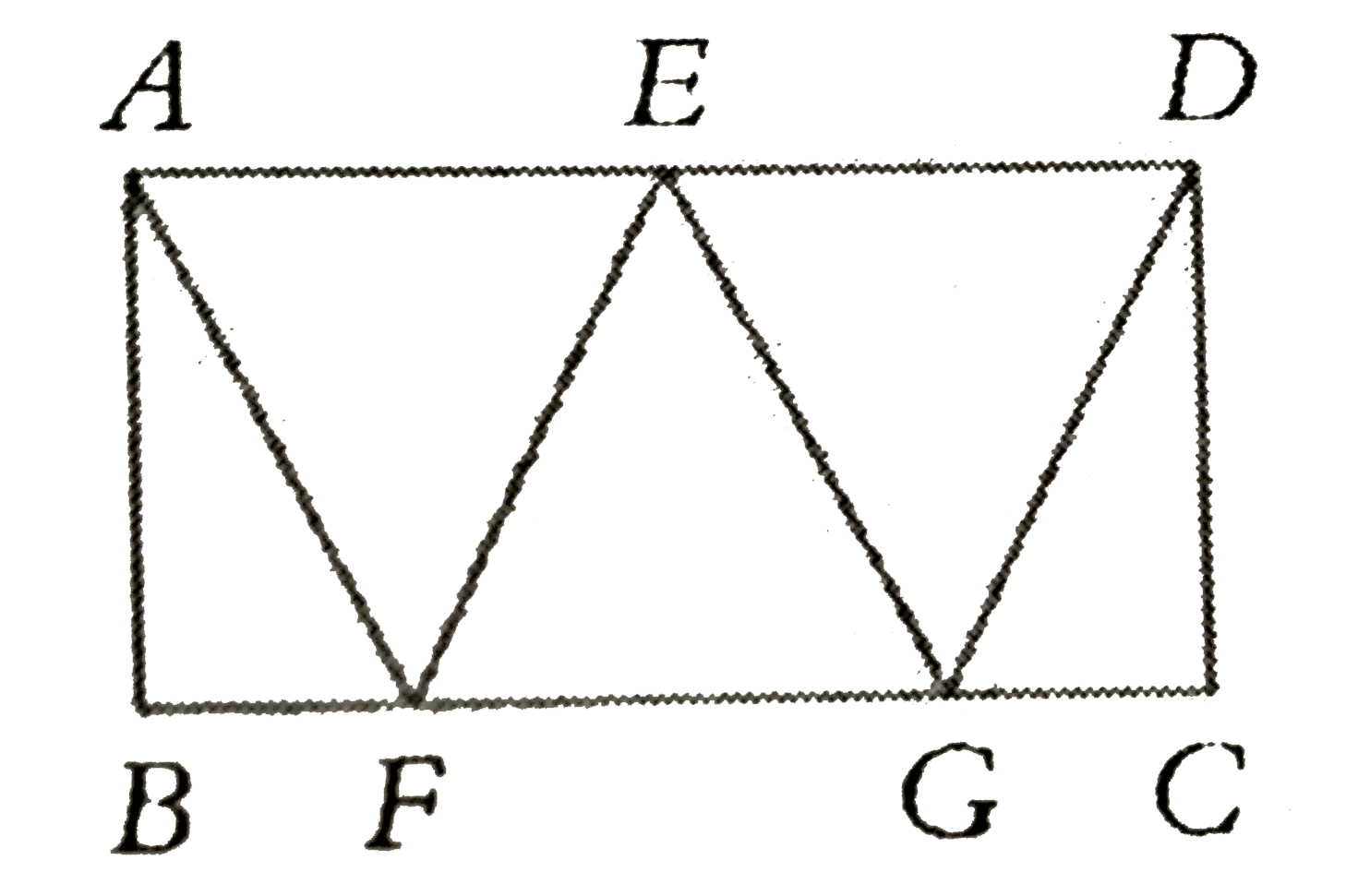In the figure above (not to scale), ¯¯¯¯¯¯EF∣∣∣∣¯¯¯¯¯¯GD,¯¯¯¯¯¯AF∣∣∣∣¯¯¯¯¯¯EG,¯¯¯¯¯¯AD∣∣¯¯¯¯¯¯BC and ∠DCG=100∘. If ∠CDG=40∘, then find ∠AEF.View Solution
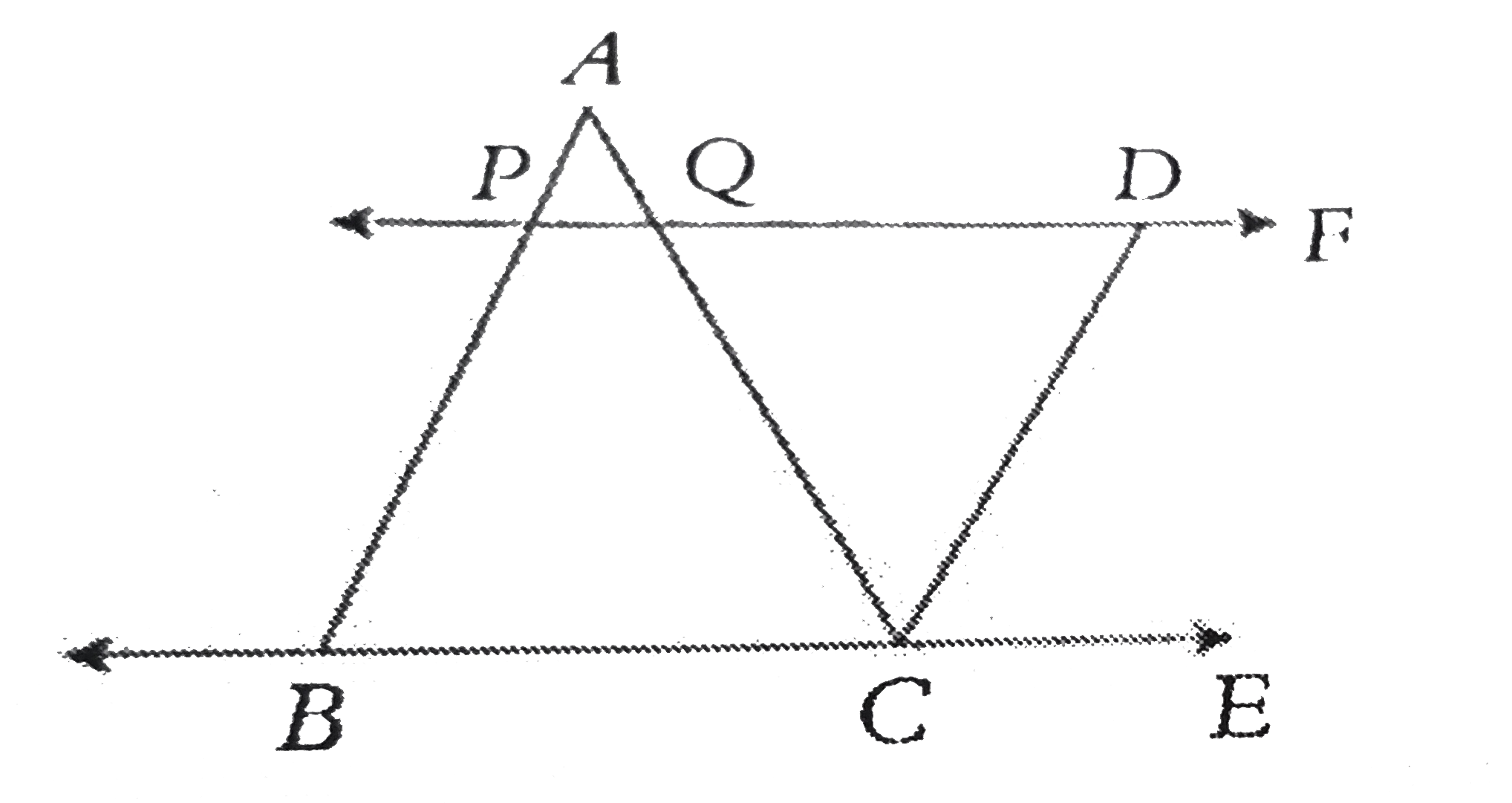In the figure above ( not to scale), ¯¯¯¯¯¯PF∣∣¯¯¯¯¯¯BE and ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. If ∠FDC=130∘ and ∠ACD=20∘, find ∠ACB and ∠ABCView SolutionIn the figure below (not to scale), ¯¯¯¯¯¯¯MR⊥¯¯¯¯¯¯¯MP,¯¯¯¯¯¯¯MQ⊥¯¯¯¯¯¯¯¯MN, and ¯¯¯¯¯¯¯MS is bisector of ∠RMQ . If ∠PMN=50∘ , then find the measure of ∠RMS.
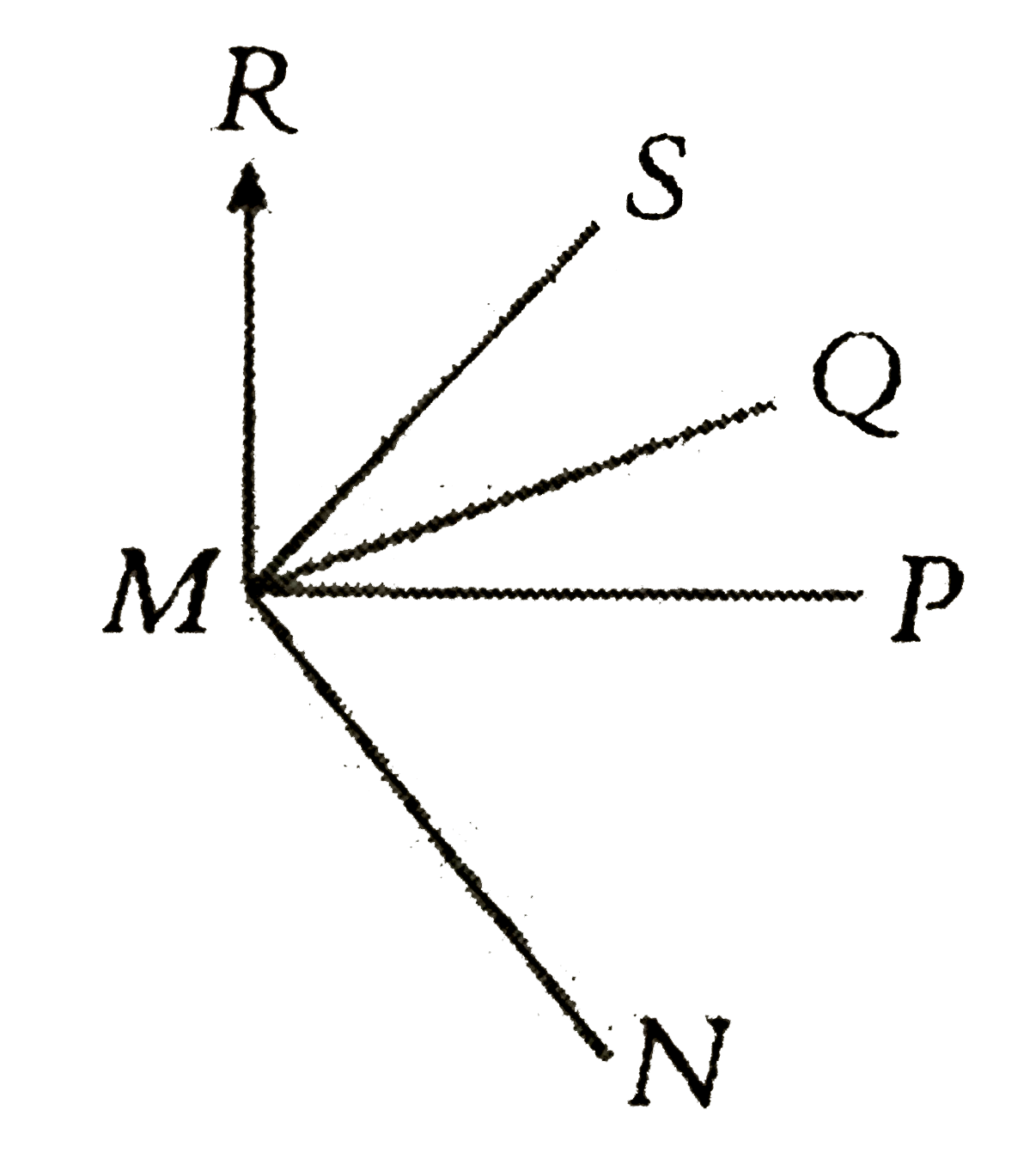View SolutionIn the following figure (not to scale), ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. If ∠BAE=25∘ and ∠DCE=30∘, then find ∠AEC.
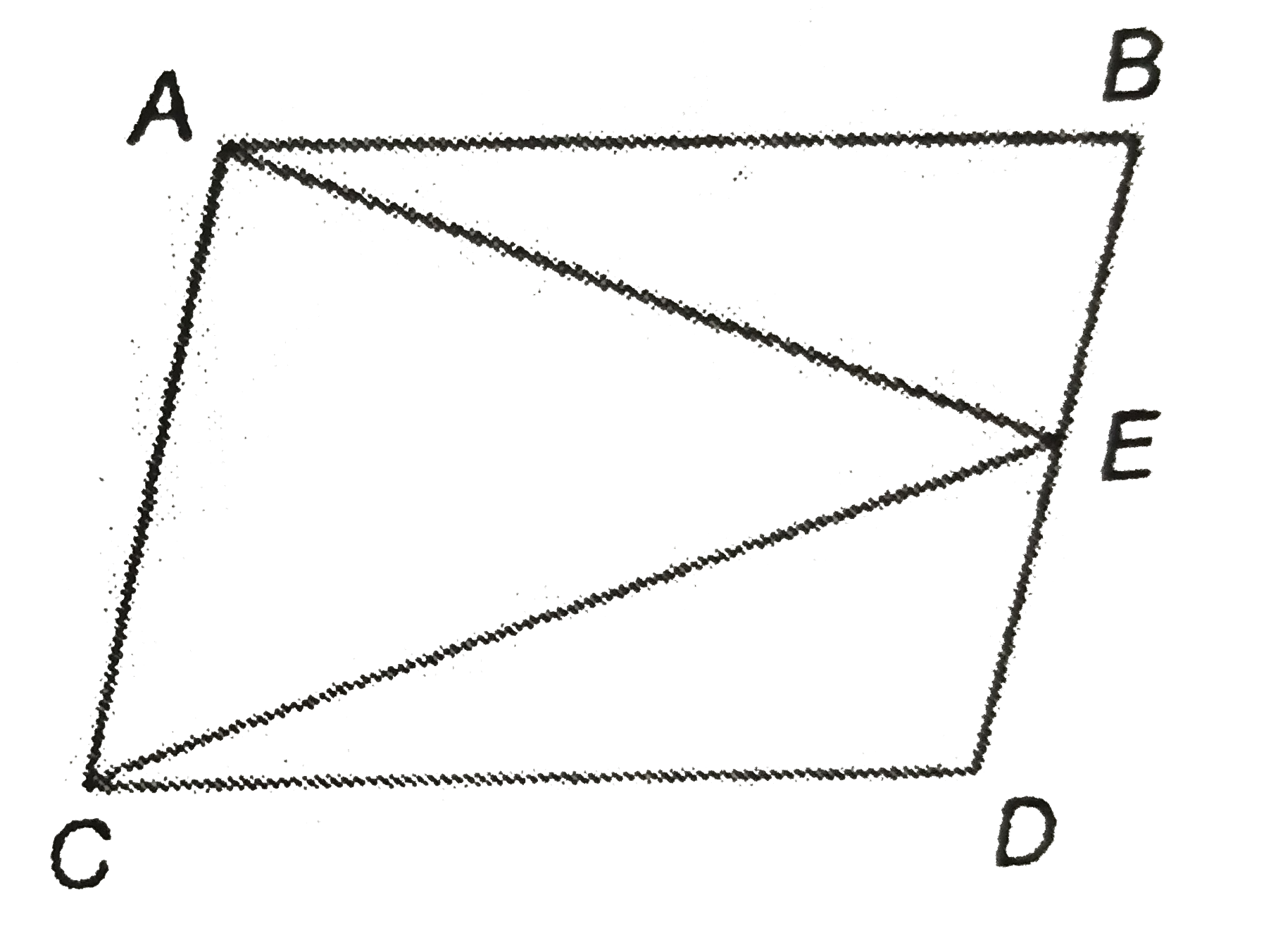View Solution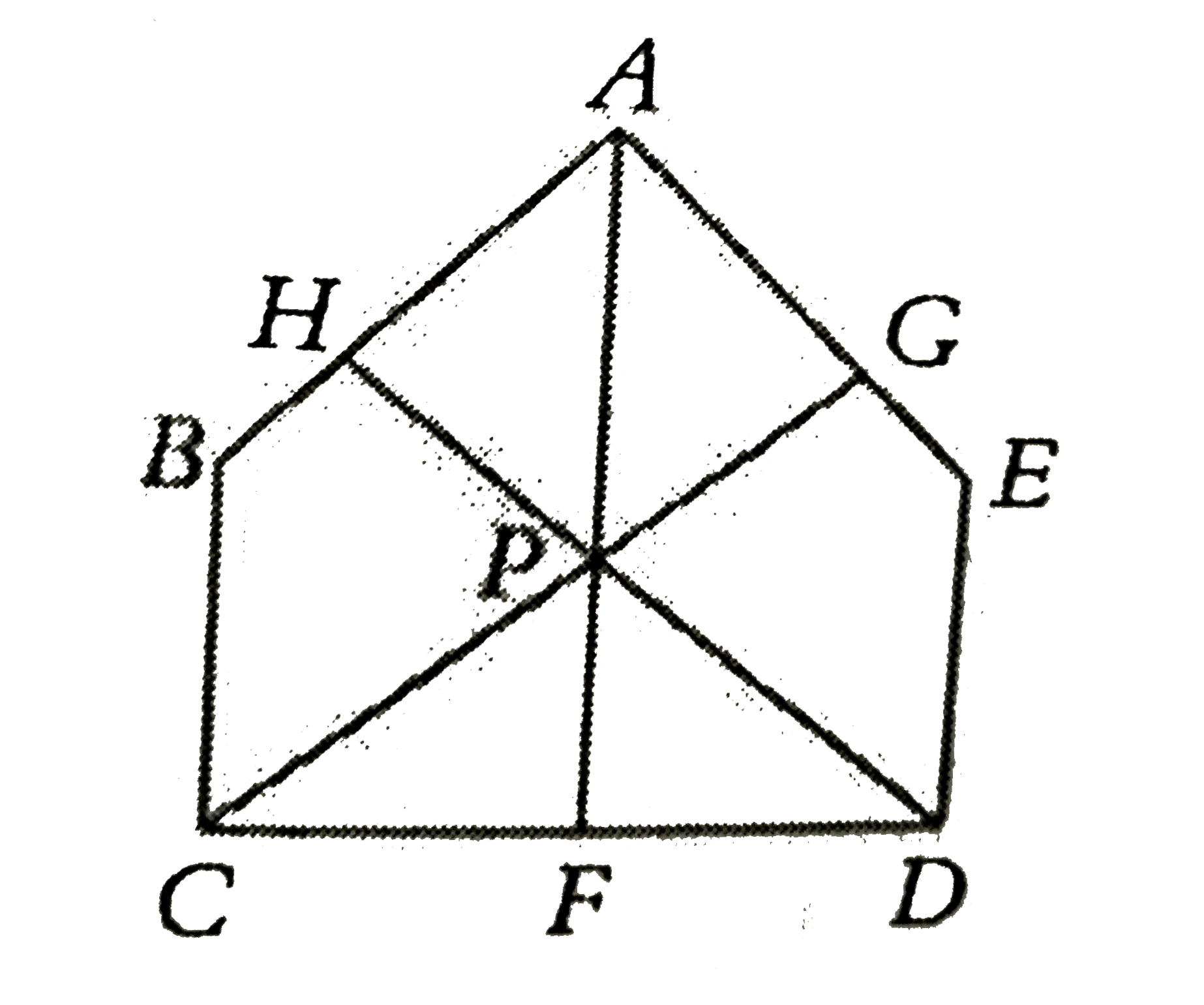
In the above figure, ¯¯¯¯¯¯AF∣∣∣∣¯¯¯¯¯¯ED,¯¯¯¯¯¯CG∣∣∣∣¯¯¯¯¯¯AB and ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯¯HD If ∠FPD=40∘, then ∠AED=View SolutionIn the figure below (not to scale) , ¯¯¯¯¯¯PQ∣∣¯¯¯¯¯TS, reflex ∠QRS=300∘ and x−y=30∘. The measure of y will be
View Solution
In the given figure, ¯¯¯¯¯¯¯LM//¯¯¯¯¯¯PN and the line l is a transversal of ¯¯¯¯¯¯¯LMand¯¯¯¯¯¯PN. Find the value of a .View Solution